10761. Сумма расстояний
Задано взвешенное дерево из n вершин и n – 1
ребер. Расстоянием
между вершинами u и v будем
называть вес наименьшего ребра на пути между u и v.
Найдите сумму расстояний между всеми
парами вершин дерева.
Вход. Первая строка содержит количество вершин
в графе n (2 ≤ n ≤ 105). Следующие n – 1 строк описывают ребра. Каждая
строка содержит три целых числа: номера вершин, соединенных ребром (вершины
пронумерованы числами от 1 до n), и вес ребра.
Выход. Выведите сумму расстояний между всеми
парами вершин дерева.
|
Пример
входа 1 |
Пример
выхода 1 |
|
3 1 2 1 1 3 3 |
5 |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
|
5 1 3 7 4 1 2 4 5 5 2 4 3 |
30 |
РЕШЕНИЕ
система
непересекающихся множеств
Анализ алгоритма
Воспользуемся
системой непересекающихся множеств. Изначально каждую вершину занесем в
отдельное множество. Будем перебирать ребра в поряде убывания их весов, для
каждого ребра (u, v) запустим функцию
Union(u, v). Она объединит множества, в которых находятся вершины u и v.
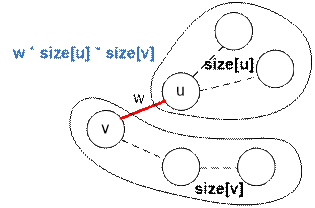
Рассмотрим текущее ребро (u,
v) дерева с весом w. Пусть оно объединяет множества с размерами
size[u]
и size[v]. Все ребра в этих двух множествах имеют вес не меньший w. Ребро (u, v) входит в size[u] * size[v] различных
путей. Поскольку вес w миинимальный,
то расстояния
этих путей равны w. То есть вклад этих
путей в сумму длин всех расстояний составляет w * size[u] * size[v].
Пример
Рассмотрим первый
тест.
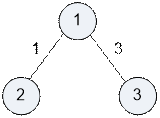
Граф содержит
три пути:
·
1 → 2 (расстояние 1);
·
1 → 3 (расстояние 3);
·
2 → 1 → 3 (расстояние 1);
Сумма расстояний
между всеми парами вершин равна 1 + 3 + 1 = 5.
Рассмотрим
второй тест.
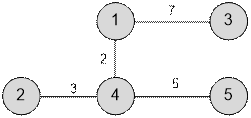
Каждую вершину отнесем к
отдельному множеству.
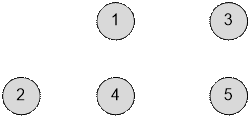
Перебираем ребра в порядке
убывания веса. Первым будет ребро (1, 3). Выполняем Union(1, 3). Расстояние 7 имеет size[1] * size[3] = 1 * 1 = 1 путь (из 1 в 3).
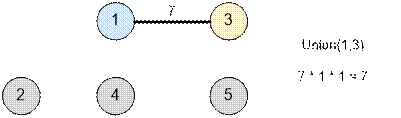
Следующим будет ребро (4, 5).
Выполняем Union(4, 5). Расстояние 5 имеет size[4] * size[5] = 1 * 1 = 1 путь (из 4 в 5).
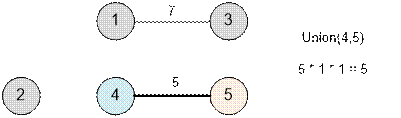
Следующим будет ребро (2, 4).
Выполняем Union(2, 4). Расстояние 3 имеет size[2] * size[4] = 1 * 2 = 2 пути (из 2 в 4 и из 2 в 5).
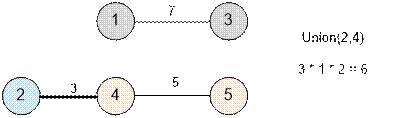
Следующим будет ребро (1, 4).
Выполняем Union(1, 4). Расстояние 2 имеет size[1] * size[4] = 2 * 3 = 6 путей (2 → 4 → 1, 4 → 1, 5 → 4 → 1, 2 → 4 → 1 → 3, 4 → 1 → 3, 5 → 4 → 1 → 3).
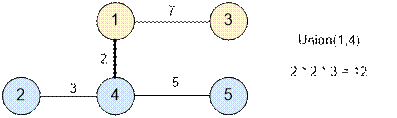
Искомая сумма
расстояний равна 7 + 5 + 6 + 12 = 30.
Реализация алгоритма
Объявим массивы, используемые системой непересекающихся множеств.
struct Edge
{
int u, v, cost;
} temp;
vector<Edge> e;
vector<int> parent, ssize;
Функция – компаратор cmpGreater сортирует ребра по
убыванию веса.
int cmpGreater(Edge a, Edge b)
{
return a.cost > b.cost;
}
Функция Repr возвращает представителя множества, в
котором находится вершина v.
int Repr(int v)
{
if (v == parent[v]) return v;
return parent[v] = Repr(parent[v]);
}
Функция Union объединяет множества с элементами x и y. Реализуем эвристику с размерами множеств.
void Union(int x, int y)
{
x = Repr(x); y = Repr(y);
if (x == y) return;
if (ssize[x] < ssize[y]) swap(x, y);
parent[y] = x;
ssize[x] += ssize[y];
}
Основная часть программы. Читаем количество вершин n в графе.
scanf("%d", &n);
Инициализируем массивы.
parent.resize(n
+ 1);
ssize.resize(n
+ 1);
for (i = 0; i <= n; i++)
{
parent[i] = i;
ssize[i] = 1;
}
Читаем ребра дерева. Сохраняем их в массиве e.
for (i = 0; i < n - 1; i++)
{
scanf("%d %d %d", &temp.u, &temp.v, &temp.cost);
e.push_back(temp);
}
Сортируем ребра по убыванию весов.
sort(e.begin(),
e.end(), cmpGreater);
В переменной res подсчитываем сумму расстояний между всеми парами вершин.
res = 0;
Перебираем ребра. Для каждого ребра (u, v) весом cost запускаем функцию
Union(u, v). В res добавляем вклад всех путей
с расстоянием cost.
for (i = 0; i < e.size(); i++)
{
res += 1LL * e[i].cost * ssize[Repr(e[i].u)] * ssize[Repr(e[i].v)];
Union(e[i].u, e[i].v);
}
Выводим ответ.
printf("%lld\n", res);
Python реализация
Объявим класс Edge, описывающий ребро
графа.
class Edge:
def
__init__(self, u, v, cost):
self.u = u
self.v = v
self.cost = cost
Функция – компаратор cmpGreater сортирует
ребра по убыванию веса.
def cmpGreater(a, b):
return
a.cost > b.cost
Функция Repr возвращает
представителя множества, в котором находится вершина v.
def Repr(v):
if
v == parent[v]: return v
parent[v] =
Repr(parent[v])
return
parent[v]
Функция Union объединяет
множества с элементами x и y. Реализуем эвристику с размерами множеств.
def Union(x, y):
x = Repr(x)
y = Repr(y)
if
x == y: return
if ssize[x] < ssize[y]:
x, y = y, x
parent[y] = x
ssize[x] +=
ssize[y]
Основная часть
программы. Читаем количество вершин n в графе.
n = int(input().strip())
Инициализируем
массивы.
parent = list(range(n + 1))
ssize = [1] * (n + 1)
e = []
Читаем ребра дерева.
Сохраняем их в списке e.
for _ in
range(n - 1):
u, v, cost = map(int, input().split())
e.append(Edge(u,
v, cost))
Сортируем ребра по
убыванию весов.
e.sort(key=lambda x: x.cost, reverse=True)
В переменной res
подсчитываем сумму расстояний
между всеми парами вершин.
res = 0
Перебираем ребра. Для
каждого ребра (u, v) весом cost запускаем функцию Union(u, v). В res добавляем вклад всех путей с расстоянием cost.
for edge in
e:
res += edge.cost *
ssize[Repr(edge.u)] * ssize[Repr(edge.v)]
Union(edge.u,
edge.v)
Выводим ответ.
print(res)