10761. Sum of distances

A weighted tree with n vertices and n – 1 edges is given. The distance between vertices u and v is defined as the weight of the smallest edge on the path between u and v.

Find the sum of distances between all pairs of vertices in the tree.

Input. The first line contains the number of vertices n (2 ≤ n ≤ 10⁵) in the graph. The next n – 1 lines describe the edges. Each line contains three integers: the numbers of vertices connected by the edge (vertices are numbered from 1 to n) and the weight of the edge.

Output. Print the sum of distances between all pairs of vertices in the tree.

Sample input 1	Sample output 1
3 1 2 1 1 3 3	5

Sample input 2	Sample output 2
5 1 3 7 4 1 2 4 5 5 2 4 3	30

SOLUTION

graphs - dsu

Algorithm analysis

Let’s use the disjoint-set data structure. Initially, each vertex will be placed in a separate set. We will iterate through the edges in decreasing order of their weights. For each edge (u, v), we will run the Union(u, v) function. It will merge the sets containing vertices u and v.

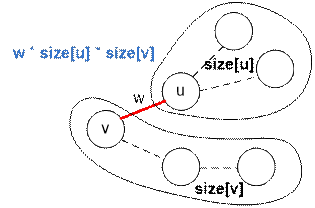
Consider the current edge (u, v) of the tree with weight w. Let it merge the sets with sizes size[u] and size[v]. All edges in these two sets have weights greater than or equal to w. The edge (u, v) is part of size[u] * size[v] different paths. Since the weight w is minimal, the distances of these paths are equal to w. Therefore, the contribution of these paths to the sum of distances of all pairs of vertices is w * size[u] * size[v].

Example

Consider the first test.

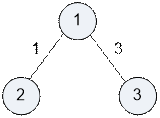
The graph contains three paths:

· 1 → 2 (distance 1);

· 1 → 3 (distance 3);

· 2 → 1 → 3 (distance 1);

The sum of distances between all pairs of vertices is equal to 1 + 3 + 1 = 5.

Consider the second test.

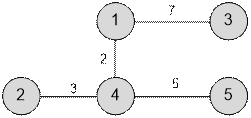
Assign each vertex to a separate set.

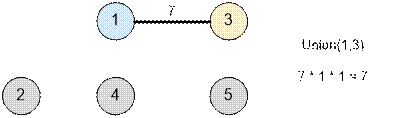
Iterate through the edges in descending order of weight. The first edge will be (1, 3). Perform Union (1, 3). The distance 7 has size[1] * size[3] = 1 * 1 = 1 path (from 1 to 3).

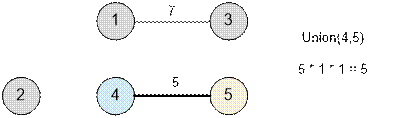
The next edge will be (4, 5). Perform Union(4, 5). The distance 5 has size[4] * size[5] = 1 * 1 = 1 path (from 4 to 5).

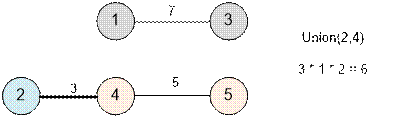
The next edge will be (2, 4). Perform Union(2, 4). The distance 3 have size[2] * size[4] = 1 * 2 = 2 paths (from 2 to 4 and from 2 to 5).

The next edge will be (1, 4). Perform Union(1, 4). The distance 2 have size[1] * size[4] = 2 * 3 = 6 paths (2 → 4 → 1, 4 → 1, 5 → 4 → 1, 2 → 4 → 1 → 3, 4 → 1 → 3, 5 → 4 → 1 → 3).

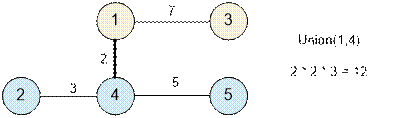
The desired sum of distances is equal to 7 + 5 + 6 + 12 = 30.

Algorithm realization

Declare arrays used by the disjoint-set system.

struct Edge

{

int u, v, cost;

} temp;

vector<Edge> e;

vector<int> parent, ssize;

The cmpGreater function is a comparator that sorts the edges in descending order of weight.

int cmpGreater(Edge a, Edge b)

{

return a.cost > b.cost;

}

The Repr function returns the representative of the set containing the vertex v.

int Repr(int v)

{

if (v == parent[v]) return v;

return parent[v] = Repr(parent[v]);

}

The Union function merges sets with elements x and y. Implement the heuristic with set sizes.

void Union(int x, int y)

{

x = Repr(x); y = Repr(y);

if (x == y) return;

if (ssize[x] < ssize[y]) swap(x, y);

parent[y] = x;

ssize[x] += ssize[y];

}

The main part of the program. Read the number of vertices n in the graph.

scanf("%d", &n);

Initialize the arrays.

parent.resize(n + 1);

ssize.resize(n + 1);

for (i = 0; i <= n; i++)

{

parent[i] = i;

ssize[i] = 1;

}

Read the edges of the tree. Store them in the array e.

for (i = 0; i < n - 1; i++)

{

scanf("%d %d %d", &temp.u, &temp.v, &temp.cost);

e.push_back(temp);

}

Sort the edges in descending order of weights.

sort(e.begin(), e.end(), cmpGreater);

Compute the sum of distances between all pairs of vertices in the variable res.

res = 0;

Iterate through the edges. For each edge (u, v) with weight cost call the Union(u, v) function. Add the contribution of all paths with distance cost to res.

for (i = 0; i < e.size(); i++)

{

res += 1LL * e[i].cost * ssize[Repr(e[i].u)] * ssize[Repr(e[i].v)];

Union(e[i].u, e[i].v);

}

Print the answer.

printf("%lld\n", res);

Python realization

Declare a class Edge, describing an edge of the graph.

class Edge:

def __init__(self, u, v, cost):

self.u = u

self.v = v

self.cost = cost

The cmpGreater function is a comparator that sorts the edges in descending order of weight.

def cmpGreater(a, b):

return a.cost > b.cost

The Repr function returns the representative of the set containing the vertex v.

def Repr(v):

if v == parent[v]: return v

parent[v] = Repr(parent[v])

return parent[v]

The Union function merges sets with elements x and y. Implement the heuristic with set sizes.

def Union(x, y):

x = Repr(x)

y = Repr(y)

if x == y: return

if ssize[x] < ssize[y]:

x, y = y, x

parent[y] = x

ssize[x] += ssize[y]

The main part of the program. Read the number of vertices n in the graph.

n = int(input().strip())

Initialize the lists.

parent = list(range(n + 1))

ssize = [1] * (n + 1)

e = []

Read the edges of the tree. Store them in the list e.

for _ in range(n - 1):

u, v, cost = map(int, input().split())

e.append(Edge(u, v, cost))

Sort the edges in descending order of weights.

e.sort(key=lambda x: x.cost, reverse=True)

Compute the sum of distances between all pairs of vertices in the variable res.

res = 0

Iterate through the edges. For each edge (u, v) with weight cost call the Union(u, v) function. Add the contribution of all paths with distance cost to res.