10762. Soldiers row

Suppose there is a row of n soldiers, identified by indices between 0 and n − 1. They are all lined up in such a way that each soldier i can see only the soldiers with indices between 0 and i − 1. We say that a soldier has clear visibility if he is at least as tall as all of those in front of him. If he doesn’t have clear visibility, it means that at least one of the others in front of him is taller.

We are interested in determining, for each soldier, whether he has clear visibility. If not, we want to identify the closest previous soldier who is taller than him.

Input. The first line contains the number of soldiers n (1 ≤ n ≤ 10⁵). The second line contains the heights of n soldiers.

Output. Print n numbers. The i-th number must contain the number of the closest previous soldier who is taller than the i-th soldier. If the i-th soldier has clear visibility, print -1.

Sample input	Sample output
10 5 3 3 4 9 2 7 5 2 4	-1 0 0 0 -1 4 4 6 7 7

SOLUTION

stack

Algorithm analysis

Declare a stack of pairs that will store information about the soldiers: the height and index. We’ll process the soldiers one by one, starting from the leftmost one. When processing the i-th soldier:

· remove from the stack the soldiers whose height does not exceed the height of the i-th soldier (i.e., those soldiers whose height is less than or equal to the height of the i-th soldier);

· the soldier at the top of the stack will be the closest previous soldier whose height exceeds the height of the i-th soldier. If the stack is empty, then the i-th soldier has a clear visibility;

· push the information about the current soldier to the stack, that is, a pair (soldier’s height, soldier’s number);

At any given moment, the stack stores soldiers sorted in descending order of their height. When a new soldier arrives, all soldiers in the stack with a height less than or equal to his are removed. Then the new soldier takes the position at the top of the stack.

Example

Let’s consider the processing of soldiers from the example.

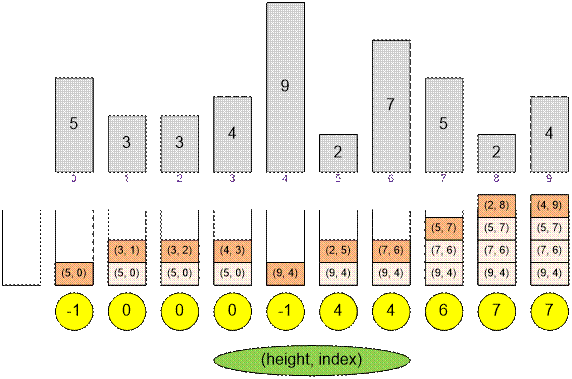
Algorithm realization

Declare a stack s to store the heights and indices of soldiers.

stack<pair<int, int> > s; // (height, index)

Read the input data.

scanf("%d", &n);

h.resize(n);

for (i = 0; i < n; i++)

scanf("%d", &h[i]);

Sequentially process n soldiers.

for (i = 0; i < h.size(); i++)

{

Remove from the stack the soldiers whose heights do not exceed the height of the i-th soldier.

while (!s.empty() && s.top().first <= h[i])

s.pop();

If the stack is empty, the i-th soldier has clear visibility. That is, he sees all the soldiers in front of him, and none of them block his view.

if (s.empty())

printf("-1 ");

else

The current soldier at the top of the stack is the closest previous soldier whose height exceeds the height of the i-th soldier.

printf("%d ", s.top().second);

Push the information about the current soldier to the stack.

s.push(make_pair(h[i], i));

}

Python realization

Read the input data.

n = int(input())

h = list(map(int, input().split()))

Declare a stack s to store the heights and indices of the soldiers.

s = []

Sequentially process n soldiers.

for i in range(len(h)):

Remove from the stack the soldiers whose heights do not exceed the height of the i-th soldier.

while s and s[-1][0] <= h[i]:

s.pop()

If the stack is empty, the i-th soldier has clear visibility. That is, he sees all the soldiers in front of him, and none of them block his view.

if not s:

print("-1", end=" ")

The current soldier at the top of the stack is the closest previous soldier whose height exceeds the height of the i-th soldier.

else:

print(s[-1][1], end=" ")

Push the information about the current soldier to the stack.

s.append((h[i], i))