10814. Disjoint Sets Union 2

Implement disjoint sets union data structure. You have to perform queries of two types:

· union u v – unite two sets that contain u and v, respectively;

· get v – find the set to which v belongs to, find the minimal and the maximal element of the set, and the total number of elements in it.

Input. The first line contains two integers n and m (1 ≤ n, m ≤ 3 * 10⁵) – the number of elements and the number of queries. Next m lines contain queries, one per line.

For a query union the line looks like union u v (1 ≤ u, v ≤ n).

For a query get the line looks like get v (1 ≤ v ≤ n).

Output. For each operation get you should output the result on a separate line in the respected order. Each result should consist of three integers: the minimal element, the maximal element, and the number of elements in the set.

Sample input	Sample output
5 11 union 1 2 get 3 get 2 union 2 3 get 2 union 1 3 get 5 union 4 5 get 5 union 4 1 get 5	3 3 1 1 2 2 1 3 3 5 5 1 4 5 2 1 5 5

SOLUTION

disjoint sets union

Algorithm analysis

Implement a disjoint sets union data structure with heuristics.

In the union operation make the recalculation of the minimum and maximum elements of a set, as well as the number of its elements.

Initially, we have n sets of one element, the i-th set contains only one number i. The minimum amin[i] and the maximum amax[i] in the i-th set are initially equal to i. The size of the i-th set cnt[i] is 1.

Let a set with a representative y be added to a set with a representative x.

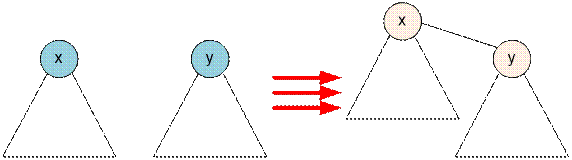
Then the minimum, maximum and number of elements in the set are recalculated as follows:

· cnt[x] = cnt[x] + cnt[y];

· amin[x] = min(amin[x], amin[y]);

· amax[x] = max(amax[x], amax[y]);

Example

Let’s simulate the queries from the sample.

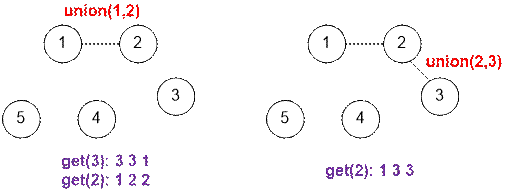
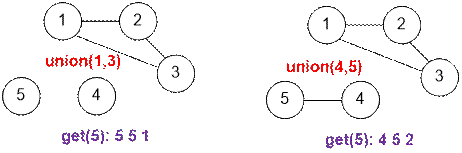
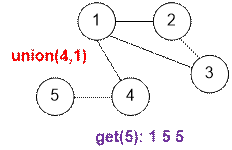
Algorithm realization

Declare the arrays:

· parent – array of parents for DSU;

· depth – contains the height of the tree, used for heuristics;

· amin, amax – arrays keep minimum and maximum elements in sets;

· cnt – an array to hold the number of elements in sets;

#define MAX 300001

int parent[MAX], depth[MAX], amin[MAX], amax[MAX], cnt[MAX];

Function Repr finds a representative of the set that contains vertex v.

int Repr(int v)

{

if (v == parent[v]) return v;

return parent[v] = Repr(parent[v]);

}

Function Union unites sets that contain vertices x and y.

void Union(int x, int y)

{

Find the representatives of x and y.

x = Repr(x), y = Repr(y);

if (x == y) return;

Implement the tree height heuristic. The set with a lower height is attached to a set with a higher height.

if (depth[x] < depth[y]) swap(x, y);

parent[y] = x;

if (depth[x] == depth[y]) depth[x]++;

The number of vertices from the set with element y is added to the set where x is located.

cnt[x] += cnt[y];

Recalculate the minimum and maximum elements in the sets.

if (amin[y] < amin[x]) amin[x] = amin[y];

if (amax[y] > amax[x]) amax[x] = amax[y];

}

The main part of the program. Read the input data. Initialize the arrays. Initially, we have n sets of one element. The minimum and maximum in the i-th set equals to i. The size of the i-th set cnt[i] is 1.

The height of each set depth[i] is initially assumed to be 0.

scanf("%d %d", &n, &m);

for (i = 1; i <= n; i++) parent[i] = i;

for (i = 1; i <= n; i++) amin[i] = amax[i] = i;

for (i = 1; i <= n; i++) cnt[i] = 1;

Process m queries sequentially.

for (i = 0; i < m; i++)

{

scanf("\n");

scanf("%s %d", s, &u);

if (s[0] == 'u')

{

scanf("%d", &v);

Union the sets that contains elements u and v.

Union(u, v);

}

else

{

Find a representative of the set containing element u.

int u1 = Repr(u);

Print the minimum and maximum element of the set, as well as the number of its elements.

printf("%d %d %d\n", amin[u1], amax[u1], cnt[u1]);

}

}