10869. Строительная
конструкция
Заданы n зданий с высотами
h1, h2, …, hn. Сделайте
так, чтобы все здания имели одинаковую высоту. Для этого разрешается как
удалять кирпичи из зданий, так и добавлять их. Каждое добавление или удаление
одного кирпича требует определённой платы, которая задаётся для каждого здания
отдельно.
Найдите минимальную общую
стоимость реконструкции, при которой все здания будут иметь одинаковую высоту k
(где k – любое целое неотрицательное число), то есть
выполняется условие h1 = h2 = ... = hn
= k.
Для простоты будем считать, что
каждое здание представляет собой вертикальную колонну из одинаковых кирпичей.
Вход. Первая строка содержит одно
целое число n (n ≤ 105) – количество зданий.
Вторая строка содержит n целых
чисел – высоты зданий h1, h2, …, hn
(0 ≤ hi ≤ 104).
Третья строка содержит n целых
чисел c1, c2, ..., cn
(0 ≤ ci ≤ 104)
– стоимость добавления или удаления одного кирпича для соответствующего здания.
Выход. Выведите одно целое число –
минимальную суммарную стоимость, за которую все здания можно сделать одинаковой
высоты.
|
Пример
входа 1 |
Пример
выхода 1 |
|
4 2 3 1 4 10 20 30 40 |
110 |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
|
3 1 2 3 10 100 1000 |
120 |
РЕШЕНИЕ
тернарный
поиск
Анализ алгоритма
Отсортируем
здания по их высотам так, чтобы выполнялось неравенство: h1 ≤ h2
≤ …≤ hn. Если несколько зданий имеют
одинаковую высоту, упорядочим их дополнительно по возрастанию стоимости
добавления или удаления кирпича.
Рассмотрим стоимость, необходимую для того, чтобы привести
все здания к высоте hx
(1 ≤ x ≤ n). Она равна
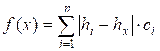
Функция
f(x), описывающая эту стоимость, является вогнутой и имеет глобальный
минимум, который можно найти с помощью тернарного поиска.
Пример
Рассмотрим первый пример. Отсортируем здания по их высотам:
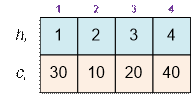
Найдём значения функции f(x) для всех возможных высот
зданий:
·
f(1) = (1 – 1) * 30 + (2 – 1) * 10 + (3 – 1) * 20 + (4 – 1) * 40
= 170,
·
f(2) = (2 – 1) * 30 + (2 – 2) * 10 + (3 – 2) * 20
+ (4 – 2) * 40 = 130,
·
f(3) = (3 – 1) * 30 + (3 – 2) * 10 + (3 – 3) * 20
+ (4 – 3) * 40 = 110,
·
f(4) = (4 – 1) * 30 + (4 – 2) * 10 + (4 – 3) * 20 + (4 – 4) * 40
= 130
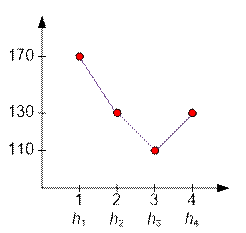
Минимальное
значение функции f(x) достигается при x = 3;
в этом случае f(3) = 110.
Реализация алгоритма
Каждое здание имеет высоту h
и стоимость cost добавления или удаления одного
этажа. Информация о зданиях хранится в массиве b.
#define MAX 100001
struct Building
{
int h, cost;
};
Building b[MAX];
Функция cmp является компаратором для сортировки
зданий. Сначала здания сортируются по возрастанию высоты, а при равных высотах –
по возрастанию стоимости.
int cmp(Building a, Building b)
{
if (a.h == b.h)
return a.cost < b.cost;
return a.h < b.h;
}
Функция f
вычисляет стоимость, необходимую для того, чтобы сделать все постройки
одинаковой высоты с высотой здания номер x.
long long f(int x)
{
long long ret = 0;
for (int i = 1; i <= n; i++)
ret += 1LL * abs(b[x].h - b[i].h) * b[i].cost;
return ret;
}
Функция ternary_search при помощи тернарного поиска ищет
такое значение x ∈ [left; right], при котором f(x) минимально. Изначально границы диапазона заданы как [left;
right] = [1; n].
long long ternarySearch(int left, int right)
{
while (right - left >= 3)
{
int a = left + (right - left) / 3;
int b = left + 2 * (right - left) / 3;
if (f(a) > f(b))
left = a;
else
right = b;
}
Разность между left и right не превышает 3. В
этом случае минимальное значение f(x) на отрезке [left; right] находим полным перебором.
long long res = f(left++);
while (left <= right)
res = min(res, f(left++));
return res;
}
Основная
часть программы. Читаем входные данные.
scanf("%d", &n);
for (i = 1; i <= n; i++)
scanf("%d", &b[i].h);
for (i = 1; i <= n; i++)
scanf("%d", &b[i].cost);
Сортируем
здания.
sort(b + 1,
b + n + 1, cmp);
Вычисляем
и выводим ответ. Здания нумеруются от 1 до n.
printf("%lld\n", ternarySearch(1, n));