10994. Монтеско
против Копулето
Ромео и Джульетта наконец-то
решили пожениться. Но приготовить свадебную вечеринку будет непросто, так как
хорошо известно, что их семьи – Монтеско и Капулето – являются кровавыми
врагами. В этой задаче Вам следует решать, кого пригласить, а кого не пригласить,
чтобы предотвратить кровопролитие.
У нас есть список n людей,
которых можно пригласить на вечеринку или нет. Для каждого человека i известен список его врагов: e1, e2, . . . , ep. Отношения “враги” обладают следующими свойствами:
Антитранзитивность. Если a враг b, а b враг c, то a друг c. Кроме того, враги друзей a – его враги, а друзья друзей a – его друзья.
Симметричность. Если a является врагом
b, то b является врагом
a (хотя это может быть и не указано в его списке врагов).
Один человек примет приглашение
на вечеринку, если и только если он приглашен, приглашены все его друзья и
никто из его врагов не приглашен. Вы должны найти максимальное количество
людей, которых можно пригласить, чтобы все они приняли приглашение.
Например, если n = 5, и мы знаем, что: 1 –
враг 3, 2 – враг
1 и 4 – враг 5, тогда мы можем пригласить
максимум 3 человек. Этими людьми могут быть 2, 3 и 4,
но для этой задачи нам нужно только количество приглашенных людей.
Вход. Первая строка содержит количество тестов m. Далее
следует пустая строка. Пустая строка также используется для разделения тестов.
Первая строка каждого теста содержит количество людей n (n ≤ 200). Для каждого из этих n людей имеется строка со списком его врагов. Первая строка содержит список
врагов человека 1, вторая строка содержит список
врагов человека 2 и так далее. Каждый список врагов начинается с
целого числа p (количество известных врагов этого человека), за которым следуют p целых чисел (p врагов этого человека). Так, например, если враги человека 5 и 7,
то список его врагов выглядит так: 2 5 7.
Выход. Для каждого теста выведите одну строку, содержащей целое
число – максимальное количество людей, которых можно
пригласить так, чтобы все они приняли приглашение.
|
Пример
входа |
Пример
выхода |
|
3 5 1 3 1 1 0 1 5 0 8 2 4 5 2 1 3 0 0 0 1 3 0 1 5 3 2 2 3 1 3 1 1 |
3 5 0 |
РЕШЕНИЕ
поиск в
глубину
Анализ алгоритма
Выделим в неориентированном графе компоненты связности.
·
Если компонента связности является
двудольной, то наибольшее количество людей, которое можно из нее пригласить, равно
числу вершин в большей двудольной компоненте.
·
Если компонента связности не является
двудольной, то людей пригласить из нее невозможно.
Пример
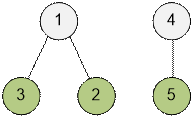
В первом тесте имеются две компоненты связности, обе из
которых двудлольные. В первой компоненте наибольшее число вершин в одной из
долей – 2 (вершины 2 и 3), во второй – 1 (вершина 5). Таким образом ответ равен 3.
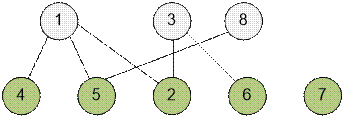
Во втором тесте можно пригласить 5 людей.
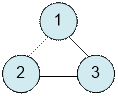
В третьем тесте имеется одна компонента связности, которая не
является двудольной.
Реализация алгоритма
Объявим матрицу смежности графа g
и массив использованных вершин used.
#define MAX 201
int g[MAX][MAX], used[MAX];
Функция dfs
запускает поиск в глубину из вершины v. Совершаем раскраску вершин двумя цветами – 1 и 2 так чтобы каждое
ребро соединяло вершины разного цвета.
·
Вершину v красим цветом color.
·
В переменной a
подсчитываем количество вершин, имеющих цвет 1.
·
Подсчитываем общее количество
вершин в текущей компоненте связности в переменной cnt.
void dfs(int v, int &a, int &cnt, int color, int &ok)
{
used[v] = color;
cnt++;
if (color == 1) a++;
for (int i = 1; i <= n; i++)
if (g[v][i] == 1)
Если вершина i
еще не посещена, то запускаем из нее поиск в глубину.
Красим ее цветом 3 – color.
if (used[i] == 0) dfs(i, a, cnt, 3 - color, ok);
else
Если граф раскрасить двумя цветами
невозможно, то он не двудольный. Установим ok
= 0.
if (used[i] == used[v]) ok = 0;
}
Основная часть программы. Читаем
входные данные. Строим граф.
scanf("%d", &tests);
while (tests--)
{
memset(g, 0, sizeof(g));
scanf("%d", &n);
for (i = 1; i <= n; i++)
{
scanf("%d", &k);
for (j = 1; j <= k; j++)
{
scanf("%d", &to);
Добавляем в граф неориентированное
ребро (i, to).
g[i][to] = g[to][i] = 1;
}
}
Запускаем поиск в глубину на
несвязном графе.
memset(used, 0, sizeof(used));
В переменной res
подсчитываем наибольшее возможное количество выбранных
вершин (приглашенных людей).
res = 0;
Перебираем вершины графа.
for (i = 1; i <= n; i++)
{
Если мы еще не были в вершине i, то запускаем из нее поиск в глубину.
if (used[i] == 0)
{
int a = 0, cnt = 0, ok = 1;
Изначально положим ok
= 1, считая что компонента связности двудольная. Вершину i красим цветом 1.
dfs(i, a, cnt, 1, ok);
Если компонента связности
двудольная (ok = 1), то размеры
ее долей равны a и cnt – a. Из двудольной компоненты мы выбираем долю с наибольшим
количеством вершин, а именно max(a, cnt – a).
res += ok * max(a, cnt - a);
}
}
Выводим ответ для текущего теста.
printf("%d\n", res);
}