10995. Квадраты и кубы

Выпишем в ряд квадраты и кубы натуральных чисел: 1, 4, 8, 9, …

Для заданного значения n требуется определить, сколько чисел от 1 до n встречаются в этом списке.

Иными словами, найдите количество таких чисел x, что x является квадратом или кубом натурального числа (в том числе и тех, которые одновременно являются и квадратами, и кубами).

Вход. В первой строке задано число тестов t.

В каждой из последующих t строк записано одно натуральное число n (1 ≤ n ≤ 10⁹).

Выход. Для каждого теста выведите в отдельной строке количество чисел от 1 до n, которые являются квадратами или кубами натуральных чисел.

Пример входа	Пример выхода
5 1 10 25 1000000 987654321	1 4 6 1090 32390

РЕШЕНИЕ

бинарный поиск

Анализ алгоритма

Сгенерируем все квадраты и кубы натуральных чисел от 1 до 10⁹ и сохраним их во множество s. Повторяющиеся числа автоматически исключатся, поскольку множество не допускает дубликатов. Затем скопируем элементы множества в массив v, который уже будет отсортирован по возрастанию, так как s – упорядоченное множество.

Далее для каждого входного числа n с помощью бинарного поиска определим количество квадратов и кубов, не превышающих n. Для этого используем поиск по верхней границе (upper_bound) – он вернёт позицию первого элемента в массиве v, строго большего n. Эта позиция и будет ответом на запрос, поскольку она соответствует количеству подходящих чисел.

Пример

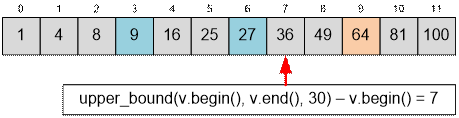
Сгенерируем квадраты и кубы чисел от 1 до 100 включительно.

Выполним запрос для n = 30. В этом случае найденная позиция будет равна pos = 7, то есть в интервале от 1 до 30 содержатся ровно 7 подходящих чисел. Напомним, что индексация в массиве v начинается с нуля.

Реализация алгоритма

Сгенерируем все квадраты и кубы натуральных чисел от 1 до 10⁹ и сохраним их во множество s. Если число одновременно является квадратом и кубом (например, 64), оно будет добавлено во множество только один раз, поскольку множества автоматически исключают повторы.

for (i = 1; i * i <= 1000000000; i++)

s.insert(i * i);

for (i = 1; i * i * i <= 1000000000; i++)

s.insert(i * i * i);

Затем перенесём элементы множества в массив v. Поскольку множество s упорядочено, массив v также будет отсортирован по возрастанию.

v = vector<int>(s.begin(), s.end());

Последовательно обрабатываем tests тестов.

scanf("%d", &tests);

while (tests--)

{

scanf("%d", &n);

При помощи бинарного поиска по верхней границе находим наименьший индекс pos такой, что все квадраты и кубы натуральных чисел, не превышающие n, находятся в массиве на позициях от 0 до pos – 1. Таким образом, количество выписанных чисел от 1 до n равно pos.

res = upper_bound(v.begin(), v.end(), n) - v.begin();

printf("%d\n", res);

}