10995. Squares and cubes
List all perfect squares and perfect cubes
of positive integers in a sequence:
1, 4, 8, 9, …
For a given value n, determine how
many numbers from 1 to n appear in this list.
In other words, find how many numbers x
satisfy the condition that x is either a square or a cube of a positive
integer (including those that are both square and cube at the same time).
Input. The first line contains the number of test cases t.
Each of the following t lines
contains a single positive integer n (1 ≤ n ≤ 109).
Output. For each test case, print on a separate line the
number of integers from 1 to n that are perfect squares or perfect cubes
of positive integers.
|
Sample
input |
Sample
output |
|
5 1 10 25 1000000 987654321 |
1 4 6 1090 32390 |
SOLUTION
binary search
Algorithm analysis
Generate all perfect squares
and cubes of positive integers from 1 to 109 and store them in a set s.
Duplicate values will be automatically eliminated, since a set does not allow
duplicates. Then, copy the elements of the set into an array v, which
will be sorted in ascending order because s is an ordered set.
Next, for each input number n,
use binary search to determine how many squares and cubes do not exceed n.
To do this, we use an upper bound search (upper_bound) – it returns the
position of the first element in array v that is strictly greater than n.
This position is the answer to the query, as it corresponds to the number of
qualifying values.
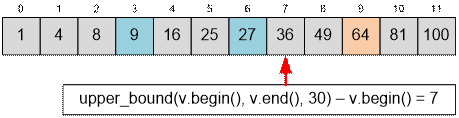
Example
Let’s
generate all perfect squares and cubes of numbers from 1 to 100 (inclusive).

Now
process the query for n = 30. In this case, the resulting position is pos
= 7, meaning there are exactly 7 such numbers in the interval from 1 to 30.
Note
that indexing in the array v starts from zero.
Algorithm implementation
Generate all perfect squares
and cubes of positive integers from 1 to 109 and store them in a set s. If a
number is both a perfect square and a perfect cube (for example, 64), it will
be added to the set only once, since sets automatically eliminate duplicates.
for (i = 1; i * i <= 1000000000; i++)
s.insert(i * i);
for (i = 1; i * i * i <= 1000000000; i++)
s.insert(i * i * i);
Then,
transfer the elements of the set into an array v. Because the set s
is ordered, the array v will also be sorted in ascending order.
v = vector<int>(s.begin(), s.end());
Process
the given number of tests sequentially.
scanf("%d", &tests);
while (tests--)
{
scanf("%d", &n);
Using
binary search with an upper bound, find the smallest index pos such that
all perfect squares and cubes of positive
integers not exceeding n are located in the
array at positions from 0 to pos – 1. Thus, the number of listed numbers from 1 to n
equals pos.
res = upper_bound(v.begin(), v.end(), n) -
v.begin();
printf("%d\n", res);
}