1033. Торт от Толи

Толя хочет угостить друзей тортом на свой день рождения. Известно, что на празднике может собраться либо n, либо m человек (включая самого именинника). На какое минимальное число частей (не обязательно равных) нужно разрезать торт, чтобы при любом из этих вариантов все получили равные доли?

Вход. Два целых числа m и n (1 ≤ m, n ≤ 30000).

Выход. Выведите минимальное количество частей, на которое необходимо разрезать торт.

Пример входа	Пример выхода
2 3	4

РЕШЕНИЕ

НОД

Анализ алгоритма

Представим торт в виде отрезка некоторой длины. Отметим на нём разрезы, соответствующие делению на n равных частей. Затем отметим разрезы, получающиеся при делении на m равных частей. Сделав все эти разрезы, мы получим именно то разбиение, которое требуется. Осталось подсчитать количество получившихся частей. Оно равно:

n + m – НОД(n, m)

Доказательство. При делении торта на n равных частей требуется n – 1 разрез. Аналогично, для m частей – m – 1 разрез. Среди них окажется НОД(n, m) – 1 совпадающих разрезов. Следовательно, всего будет сделано

(n – 1) + (m – 1) – (НОД(n, m) – 1) = n + m – 1 – НОД(n, m)

различных разрезов. После этого торт разделится на n + m – НОД(n, m) частей.

Пример

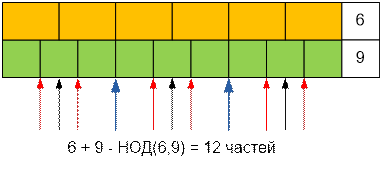
При разрезании торта на 6 частей требуется 5 разрезов.

При разрезании торта на 9 частей требуется 8 разрезов.

Из них совпадают НОД(6, 9) – 1 = 2 разреза.

Таким образом, на торте получится 5 + 8 – 2 = 11 различных разрезов. После их выполнения торт разделится на 12 кусков.

Реализация алгоритма

Функция gcd вычисляет наибольший общий делитель двух чисел a и b.

int gcd(int a, int b)

{

return (!b) ? a : gcd(b,a % b);

}

Основная часть программы. Читаем входные данные.

scanf("%d %d",&m,&n);

Вычисляем и выводим ответ.

res = m + n - gcd(m,n);

printf("%d\n",res);

Java реализация

import java.util.*;

public class Main

{

static int gcd(int a, int b)

{

return (b == 0) ? a : gcd(b,a % b);

}

public static void main(String []args)

{

Scanner con = new Scanner(System.in);

int m = con.nextInt();

int n = con.nextInt();

int res = m + n - gcd(m,n);

System.out.println(res);

con.close();

}

}

Python реализация

Функция gcd вычисляет наибольший общий делитель двух чисел a и b.

def gcd(a, b):

if a == 0: return b

if b == 0: return a

if a > b: return gcd(a % b, b)

return gcd(a, b % a)

Основная часть программы. Читаем входные данные.

m, n = map(int, input().split())

Вычисляем и выводим ответ.

res = m + n - gcd(m, n)

print(res)