1033. Cake from Tolya

Tolya wants to treat his friends to a cake on his birthday. It is known that there may be either n or m people at the party (including the birthday person). What is the minimum number of pieces (not necessarily equal) into which the cake should be cut so that in either case everyone gets an equal share?

Input. Two integers m and n (1 ≤ m, n ≤ 30000).

Output. Print the minimum number of pieces into which the cake should be cut.

Sample input	Sample output
2 3	4

SOLUTION

GCD

Algorithm analysis

Let us represent the cake as a line segment of some length. Mark the cuts corresponding to dividing it into n equal parts. Then mark the cuts corresponding to dividing it into m equal parts. Making all these cuts will give us exactly the required partition. It remains to count the number of resulting pieces. This number is:

n + m – GCD(n, m)

Proof. Dividing the cake into n equal parts requires n – 1 cuts. Similarly, dividing it into m parts requires m – 1 cuts. Among them, there will be GCD(n, m) – 1 coinciding cuts. Therefore, the total number of distinct cuts is

(n – 1) + (m – 1) – (GCD(n, m) – 1) = n + m – 1 – GCD(n, m)

After making these cuts, the cake will be divided into n + m – GCD(n, m) pieces.

Example

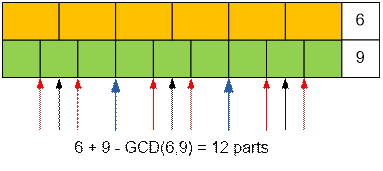
When cutting the cake into 6 pieces, 5 cuts are required.

When cutting the cake into 9 pieces, 8 cuts are required.

Among them, GCD(6, 9) – 1 = 2 cuts coincide.

Thus, the cake will have 5 + 8 – 2 = 11 distinct cuts. After making them, the cake will be divided into 12 pieces.

Algorithm implementation

The function gcd computes the greatest common divisor of the numbers a and b.

int gcd(int a, int b)

{

return (!b) ? a : gcd(b,a % b);

}

The main part of the program. Read the input data.

scanf("%d %d",&m,&n);

Compute and print the answer.

res = m + n - gcd(m,n);

printf("%d\n",res);

Java implementation

import java.util.*;

public class Main

{

static int gcd(int a, int b)

{

return (b == 0) ? a : gcd(b,a % b);

}

public static void main(String []args)

{

Scanner con = new Scanner(System.in);

int m = con.nextInt();

int n = con.nextInt();

int res = m + n - gcd(m,n);

System.out.println(res);

con.close();

}

}

Python implementation

The function gcd computes the greatest common divisor of the numbers a and b.

def gcd(a, b):

if a == 0: return b

if b == 0: return a

if a > b: return gcd(a % b, b)

return gcd(a, b % a)

The main part of the program. Read the input data.

m, n = map(int, input().split())

Compute and print the answer.

res = m + n - gcd(m, n)

print(res)