1043. Геометрический
парадокс
На рисунке ниже
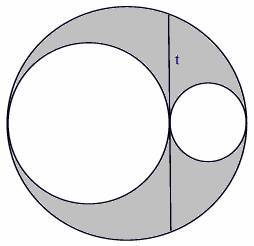
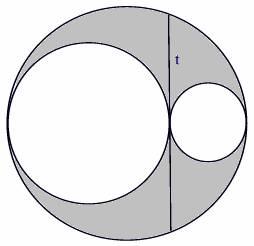
Вы видите два меньших круга, касающихся внешне друг друга. Больший круг
расположен так, что он также касается этих двух кругов, но меньшие круги
расположены внутри него. Хорда t большего
круга является общей касательной к двум меньшим кругам радиусами r1 и r2. Центры всех трёх окружностей лежат на одной прямой.
Вам заданны значения радиусов кругов r1
и r2, или значение длины
хорды t. Вам необходимо вычислить
значение площади большего круга, помеченной серым цветом на риcунке. Если
заданной информации не достаточно для однозначного определения указанной
площади, необходимо вывести сообщение "Impossible."
Вход. Первая строка содержит количество тестов n (n ≤ 100). Каждая следующая строка содержит или два целых числа (r1 и r2) или одно t. Все числа
целые, меньше 100.
Выход. Для каждого набора входных данных выведите одну строку.
Она должна содержать площадь серой области, если входных данных достаточно для
её нахождения. В противном случае выведите единственное слово “Impossible.” Площадь следует
выводить с четырьмя десятичными знаками.
|
Пример
входа |
Пример
выхода |
210 10
15
20 |
628.3185 1884.9556 |
РЕШЕНИЕ
геометрия
Анализ алгоритма
Решение задачи
существует всегда, то есть фраза “Impossible.” выводиться никогда не будет.
Радиус большей
окружности равен r = r1 + r2. Если значения r1 и r2 известны, то площадь серой части
равна π((r1 + r2)2 – r12 – r22) = 2πr1r2.
Пусть нам
известно только значение t.
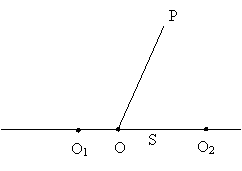
Рассмотрим прямоугольный треугольник OPS. В нем OP = r1 + r2, OS = r1 + r2 – 2r2
= r1 – r2, SP = t / 2. Запишем теорему
Пифагора:
(r1 + r2)2 = (r1 – r2)2 + t2 / 4
Раскрывая
скобки, получим 2 r1 r2 = – 2 r1 r2 + t2 / 4, 4 r1 r2 = t2 / 4.
Площадь серой
части равна 2πr1r2 = π t2 / 8.
Реализация алгоритма
Читаем входные
данные.
scanf("%d",&n);
while(n--)
{
scanf("%d",&r1);scanf("%c",&c); cnt = 1;
if (c == ' ')
scanf("%d\n",&r2),
cnt = 2;
Вычисляем площадь серой области
согласно выше приведенным формулам.
if (cnt == 2)
res = 2*PI*r1*r2; else res = PI * r1 * r1 / 8;
printf("%.4lf\n",res);
}