1070. Закраска прямой

На числовой прямой окрашены n отрезков. Известны координаты левого и правого концов каждого отрезка l_i и r_i. Найдите длину окрашенной части числовой прямой.

Вход. В первой строке находится число n (1 ≤ n ≤ 15000). В следующих n строках расположены целые числа l_i и r_i (-10⁹ ≤ l_i ≤ r_i ≤ 10⁹) – координаты концов отрезков.

Выход. Выведите длину окрашенной части числовой прямой.

Пример входа	Пример выхода
5 6 8 1 2 0 3 7 9 2 4	7

РЕШЕНИЕ

геометрия – заметание на прямой

Анализ алгоритма

Занесем точки – концы n отрезков – в массив v, запомнив при этом каким концом (левым или правым) они являются. Затем отсортируем 2 * n точек по их абсциссе v[i]. Будем двигаться слева направо по интервалам (v[i], v[i + 1]) между точками, организовав движение заметающей прямой.

Будем поддерживать переменную depth, равную количеству отрезков, покрывающих интервал (v[i], v[i + 1]). Изначально присвоим ей значение 0. Значение depth будем увеличивать на 1, когда встречается точка, являющаяся началом отрезка, и уменьшать на 1, когда точка является концом отрезка.

Длина окрашенной части прямой равна сумме длин интервалов x_i+1 – x_i, на которых depth ≠ 0.

Пример

Рассмотрим набор следующих отрезков:

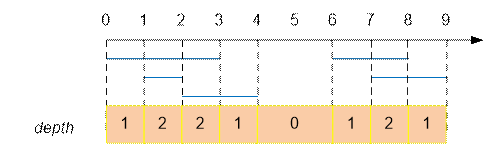
Ответом является сумма длин интервалов x_i+1 – x_i, на которых depth не равно нулю.

Реализация алгоритма

Точки – концы отрезков – будем хранить в массиве v в виде пар: (абсцисса x точки, метка – начало или конец отрезка).

vector<pair<int, int> > v; // (x, flag), flag: 0 = Left, 1 = Right

Читаем отрезки и формируем массив точек.

scanf("%d", &n);

for (i = 0; i < n; i++)

{

scanf("%d %d", &Left, &Right);

v.push_back({Left, 0}); // начало отрезка

v.push_back({Right, 1}); // конец отрезка

}

Сортируем точки по абсциссе.

sort(v.begin(), v.end());

Глубину перекрытия отрезков (количество отрезков на рассматриваемом интервале) поддерживаем в переменной depth.

depth = 0;

Длину окрашенной части прямой вычисляем в переменной res.

res = 0;

Двигаемся по точкам слева направо. Для каждого значения i рассматриваем интервал [v[i].first, v[i + 1].first].

· Если v[i] является началом отрезка, то увеличиваем depth на 1.

· Если v[i] является концом отрезка, то уменьшаем depth на 1.

Если на текущем интервале depth > 0, то интервал считается окрашенным. Его длину прибавляем к res.

Поскольку массив v содержит 2 * n точек, в цикле будет рассмотрено 2 * n – 1 интервал.

for (i = 0; i < v.size() - 1; i++)

{

if (v[i].second == 0) depth++; else depth--;

if (depth > 0) res += v[i + 1].first - v[i].first;

}

Выводим ответ.

printf("%d\n", res);

Реализация алгоритма – класс

Объявим класс Point, в котором хранится абсцисса x точки и метка c (которая указывает, является ли точка началом или концом отрезка).

class Point

{

public:

int x;

char c; // 'b' – начало отрезка, 'e' – конец отрезка

Point(void)

{

x = 0; c = '-';

}

Point(int x, char c) : x(x), c(c) {};

};

Point p[MAX];

Функция f является компаратором для сортировки точек по абсциссе.

int f(Point a, Point b)

{

return a.x < b.x;

}

Основная часть программы. Читаем отрезки, формируем массив точек.

scanf("%d",&n);

for(i = 0; i < 2 * n; i += 2)

{

scanf("%d %d",&x,&y);

p[i] = Point(x,'b');

p[i+1] = Point(y,'e');

}

Сортируем точки по абсциссе.

sort(p, p + 2 * n, f);

Моделируем движение заметающей прямой слева направо.

depth = len = 0;

for(i = 0; i < 2 * n - 1; i++) // двигаемся по отрезку [p[i]...p[i+1]

{

if (p[i].c == 'b') depth++;

if (p[i].c == 'e') depth--;

if (depth > 0) len += p[i+1].x - p[i].x;

}

Выводим ответ.

printf("%d\n",len);