1070. Fill the line

 

n segments are painted on the line. The coordinates of the left and right ends of each segment li and ri are known. Find the length of the colored part of the line.

 

Input. The first line contains the number n (1 ≤ n ≤ 15000), the following n lines contains the pair of integers li and ri (-109 ≤ li ≤ ri ≤ 109).

 

Output. Print the length of the colored part of the line.

 

Sample input

Sample output

5

6 8

1 2

0 3

7 9

2 4

7

 

 

 

SOLUTION

geometry – sweeping line

 

Algorithm analysis

Store the points – the ends of n segments into the array v, marking which end (left or right) they are. Then sort 2 * n points by the abscissa v[i]. Now move from left to right along the intervals (v[i], v[i + 1]) between the points (we’ll organize the movement of the sweeping line). Keep the variable depth equal to the number of segments covering the interval (v[i], v[i + 1]). Initially, set it to 0. The value depth will be increased by 1 if the point is the start of segment, and decreased by 1 if the point is the end of segment.

The length of the colored part of the straight line equals to the sum of the lengths of the intervals xi+1 – xi, where depth is not zero.

 

Example

Consider a set of the following line segments:

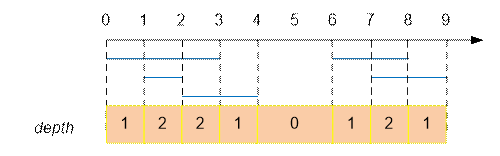
The answer is the sum of the lengths of the intervals xi+1 – xi, where depth is not zero.

 

Algorithm realization

The points – the ends of segments – will be stored in an array of pairs v: (abscissa x of the point, and the label – the start or the end of a segment).

 

vector<pair<int, int> > v; // (x, flag), flag: 0 = Left, 1 = Right

 

Read the segments, construct an array of points.

 

scanf("%d", &n);

for (i = 0; i < n; i++)

{

  scanf("%d %d", &Left, &Right);

  v.push_back(make_pair(Left, 0)); // start of a segment

  v.push_back(make_pair(Right, 1)); // end of a segment

}

 

Sort the points by abscissa.

 

sort(v.begin(), v.end());

 

The depth of segments overlapping (the number of segments in the considered interval) is maintained in the variable depth.

 

depth = 0;

 

The length of the painted part of the straight line is computed in the variable res.

 

res = 0;

 

Move along the points from left to right. For each value of i, consider the interval [v[i].first, v[i + 1].first]. If point v[i] is the start of segment (v[i].second = 0), then increase depth by 1. If v[i] is the end point, then decrease depth by 1. If depth > 0 at the current interval, then interval is painted. Add its length to res.

Since array v contains 2 * n points, the loop will iterate over 2 * n – 1 intervals.

 

for (i = 0; i < v.size() - 1; i++)

{

  if (v[i].second == 0) depth++; else depth--;

  if (depth > 0) res += v[i + 1].first - v[i].first;

}

 

Print the answer.

 

printf("%d\n", res);

 

Algorithm realization – class

Declare the class point, that stores its abscissa x and label c (whether the point is the start or the end of a segment)

 

class Point

{

public:

  int x;

  char c; // 'b' – start of segment, 'e' – end of segment

  Point(void)

  {

    x = 0; c = '-';

  }

  Point(int x, char c) : x(x), c(c) {};

};

 

Point p[MAX];

 

The function of sorting points by abscissa.

 

int f(Point a, Point b)

{

  return a.x < b.x;

}

 

The main part of the program. Read the segments, construct an array of points.

 

scanf("%d",&n);

for(i = 0; i < 2*n; i+=2)

{

  scanf("%d %d",&x,&y); 

  p[i] = Point(x,'b');

  p[i+1] = Point(y,'e');

}

 

Sort the points by abscissa.

 

sort(p,p+2*n,f);

 

Simulate the movement of the sweeping line from left to right.

 

depth = len = 0;

for(i = 0; i < 2*n - 1; i++) // move along the interval [p[i]...p[i+1]

{

  if (p[i].c == 'b') depth++;

  if (p[i].c == 'e') depth--;

  if (depth > 0) len += p[i+1].x - p[i].x;

}

 

Print the answer.

 

printf("%d\n",len);