1079. Removing the letters

You are given two words (each word consists of upper-case English letters). Delete some letters from each word so that the resulting words become equal.

Find the maximum possible length of the resulting word.

Input. Each test case consists of a single line, containing two words separated by a space. The length of each of these words is between 1 and 200. There are no more than 10 test cases.

Output. For each test case output the maximum length of a resulting word (the length of the longest word that can be created from both words by removing some letters).

If two words have no letters in common, print 0.

Sample input	Sample output
AAABBB ABABAB AXYAAZ CXCYCZC ABCDE EDCBA	4 3 1

SOLUTION

dynamic programming - LCS

Algorithm analysis

The answer to the problem is the length of the longest common subsequence (LCS) of input sequences of uppercase Latin letters.

Let f(i, j) be the longest common subsequence of sequences x₁x₂…x_i and y₁y₂…y_j.

If x_i ¹ y_j, then find LCS between x₁x₂…x_i-1 and y₁y₂…y_j, and also between x₁x₂…x_i and y₁y₂…y_j-1. Return the largest of them:

f(i, j) = max( f(i, j – 1), f(i – 1, j) )

If x_i = y_j, then find LCS between x₁x₂…x_i-1 and y₁y₂…y_j-1:

f(i, j) = 1 + f(i – 1, j – 1)

The values f(i, j) will be stored in array m[0.. SIZE, 0.. SIZE], where m[0][i] = m[i][0] = 0. Since the length of words is no more than 200 characters then assign SIZE = 201.

Each next line of array m[i][j] is calculated through the previous one. Therefore, to find the answer, it is enough to keep only two lines in memory.

Example

Here is given the largest common subsequences for samples.

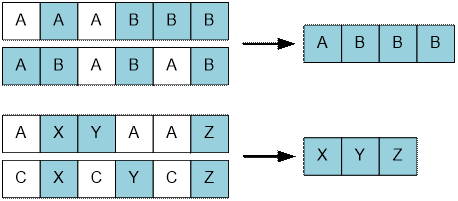
Algorithm realization

Strings x and y contain input sequences, lenx and leny are their lengths. Array m contains the last two lines of dynamic computations.

#define SIZE 1001

string x, y;

int m[2][SIZE];

int lenx, leny;

Input data are processed till the end of file. Read two input sequences into strings x and y. We add a space before the strings, so that the sequences will start from the first position. Store the positions of the last characters in the strings in the variables lenx and leny.

while (cin >> x >> y)

{

x = ' ' + x; lenx = x.size() - 1;

y = ' ' + y; leny = y.size() - 1;

Set array m to zero. Dynamically compute the values of f(i, j). Initially, m[0][j] contains the values f(0, j). Further, in m[1][j] we store the values of f(1, j). Since to calculate f(2, j) it is enough to have the values of two previous rows of array m, then the values f(2, j) can be stored in cells m[0][j], the values f(3, j) can be stored in cells m[1][j] and so on.

memset(m,0,sizeof(m));

for(i = 1; i <= lenx; i++)

for(j = 1; j <= leny; j++)

if (x[i] == y[j]) m[i % 2][j] = 1 + m[(i-1)%2][j-1];

else m[i % 2][j] = max(m[(i-1)%2][j],m[i%2][j-1]);

At the end of the algorithm, the length of the longest common subsequence will be in the cell m[lenx%2][leny]. Print it.

cout << m[lenx % 2][leny] << endl;

}