1087. Mötərizə ardıcıllığı

Düzgün mötərizəli ifadəyə aşağıdakı kimi tərif verək:

1. Boş ifadə -düzgündür.

2. Əgər S düzgündürsə, onda (S) və [S] –də düzgündür.

3. Əgər A və B ifadəəri düzgündürsə, onda AB –də düzgündür.

(, ), [, və ] simvollarından ibadət ardıcıllıq verimişdir. Elə ən qısa düzgün mötərizə ifadəsi tapmaq tələb olunur ki, verilmiş ifadə onun alt ifadəsi olsun. Başqa sözlə elə düzgün mötərizə ifadəsi tapmaq tələb olunur ki, ondakı bəzi simvolları pozaraq eynilə verilmiş ifadə alınsın.

Giriş. Birinci sətirdə, uzunluğu 100 –ü aşmaayan (, ), [, və ] simvollarından ibadət ardıcıllıq veriir.

Çıxış. Axtarılan boşluqsuz mötərizəli ifadə çıxışa verilir.

Girişə nümunə

([(]

Çıxışa nümunə

()[()]

Həlli

dinamik proqramlama

Alqoritmin analizi

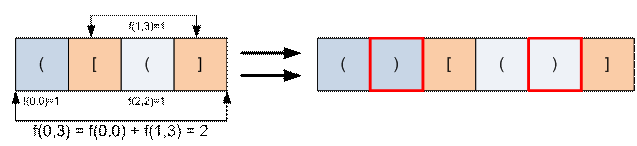
Tutaq ki, S = s₀s₁…s_n-1 – giriş sətridir. dp[i][j] ən az saylı simvollar sayıdır ki, onları s_i…s_j –yə əlavə etməklə düzgün ifadə alınar. Təbiidir ki, s_i mötərizələrinin tipindən asılı olmayaraq dp[i][i] = 1 olar. i > j halı üçün dp[i][j] = 0 götürək.

· Əgər s_i = s_j isə, onda dp[i][j] = min(dp[i][j], dp[i + 1][j – 1]);

· Əgər s_i ≠ s_j isə, onda dp[i][j] = (dp[i][j], dp[i][k] + dp[k + 1][j]);

Yekun sətrin tərtib olunması üçün məlumatlar P massivində saxlanacaq. Qeyd edək ki,

· p[i][j] = -1, əgər s_i = s_j və minimum dp[i][j] , dp[i + 1][j – 1] –də alınır;

· p[i][j] = k, əgər minimum dp[i][j], dp[i][k] + dp[k + 1][j] –toplananlarında alınırsa;

Alqoritmin realizə olunması

Konstant və işçi massivləri təyin edək.

#define MAX 110

#define INF 0x3F3F3F3F

char s[MAX];

int dp[MAX][MAX], p[MAX][MAX];

i-ci mövqedən j-ciyə qədər nəticə sətrin çıxarılması .

void Print(int i, int j)

{

if (i > j) return;

if (i == j)

{

if (s[i] == '(' || s[i] == ')')

printf("()");

else

printf("[]");

} else if (p[i][j] == -1)

{

printf("%c", s[i]);

Print(i + 1, j - 1);

printf("%c", s[j]);

} else

{

Print(i, p[i][j]);

Print(p[i][j] + 1, j);

}

}

Solve(i, j) funksiyasının köməyilə, düzgün alt sətrə çevirmək üçün s_i…s_j –yə əlavə olunması lazım olan minimal simvol sayı dp[i][j] ilə tapılır. Eyni zamanda yekun sətri almaq üçün p massivini də doldururuq.

int Solve(int i, int j)

{

if (i == j) return 1;

if (i > j) return 0;

if (dp[i][j] != INF) return dp[i][j];

if ((s[i] == '(' && s[j] == ')') || (s[i] == '[' && s[j] == ']'))

dp[i][j] = min(dp[i][j], Solve(i+1,j-1));

for (int k = i; k < j; k++)

{

int temp = Solve(i,k) + Solve(k+1,j);

if (temp < dp[i][j])

{

p[i][j] = k;

dp[i][j] = temp;

}

}

return dp[i][j];

}

Proqramın əsas hissəsi. S sətrini oxuyuruq..

gets(s); len = strlen(s);

memset(dp,0x3F,sizeof(dp));

memset(p,-1,sizeof(p));

Cavabı hesablayıb çıxarırıq..

Solve(0, len - 1);

Print(0, len - 1);

printf("\n");