11058. Chasing a
butterfly
On clear summer days, Nyusha enjoys
catching butterflies in the fresh air. But today, she encountered a
particularly cunning butterfly – it
flew into a labyrinth and tried to hide from her inside.
The labyrinth consists of n rooms,
numbered from 1 to n, some of which are connected by corridors. It is
known that there is exactly one simple path between any two rooms, passing only
through the corridors. In other words, the labyrinth forms a tree with n vertices
and n − 1 edges.
The entrance to the labyrinth is located in
room number 1. A leaf is defined as any room connected to exactly one other
room and not being the root (i.e., not room 1). Each leaf contains an exit from
the labyrinth. The butterfly starts its flight from room 1, heading toward one
of the exits. It moves at a constant speed, never turns around, and travels
through one corridor per minute, moving to a neighboring room. All corridors
are of equal length.
To catch the butterfly, Nyusha decided to
enlist the help of some friends. Initially, each of them can take position in
any room that contains an exit. As soon as the butterfly begins its journey
from the entrance toward some exit, the friends may immediately start moving
from their rooms toward the entrance. They move at the same speed as the
butterfly. If any of them encounters the butterfly – whether
in a room or in the middle of a corridor – it is
considered caught. However, if the butterfly reaches an exit without
encountering any of the friends, it successfully escapes to freedom.
Help Nyusha determine the minimum number of
friends needed to guarantee catching the butterfly, regardless of which exit it
chooses.
Input. The first line contains a single integer n (2 ≤ n ≤ 200000) – the number of rooms in the labyrinth.
The following n
– 1 lines describe the corridors connecting the rooms. Each line contains two
integers u and v (1 ≤ u, v ≤ n, u ≠ v) – the indices of the rooms connected by a corridor.
It is guaranteed that the given corridor
system forms a tree.
Output. Print a single integer – the
minimum number of friends required to guarantee that the butterfly will be
caught.
|
Sample
input 1 |
Sample
output 1 |
|
3 1 2 1 3 |
2 |
|
|
|
|
Sample
input 2 |
Sample
output 2 |
|
4 1 2 2 3 2 4 |
1 |
SOLUTION
graphs – dfs
Algorithm analysis
Perform
a depth-first search starting from vertex 1. For each vertex, compute two
values:
·
d[v] – the distance from
vertex 1 to vertex v. If p is the parent of v, then
d[v]
= d[p] + 1
·
h[v] – the distance from
vertex v to the nearest leaf in the subtree rooted at v. If to1,
to2, …, tok are the children of vertex v, then
h[v]
= 1 + min(h[to1], h[to2], …, h[tok])
·
If v is a leaf of the tree,
set h[v]
= 0.
Next,
perform a second depth-first search. During this traversal, compute the value
res[v] – the minimum number of friends that need to be placed in some of
the leaves of the subtree rooted at vertex v in order to guarantee
catching the butterfly, assuming it chooses to fly into this subtree.
If h[v] ≤ d[v], then res[v] = 1. In this case, it is enough to place
one friend in the leaf with the minimal depth in the subtree rooted at vertex v:
they will reach vertex v no later than the butterfly flying from the
root.
Otherwise,
if to1, to2, …, tok are
the children of vertex v, then
res[v]
= res[to1] + res[to2] + … + res[tok]
If
the butterfly is not caught at vertex v itself, we must be prepared to
intercept it in any of the subtrees of v’s children.
The
final answer to the problem is the value res[1].
Example
In
the first example (shown in the left diagram), two friends are required, and
they should be placed at the two exits. The butterfly can fly from vertex 1
either to vertex 2 or to vertex 3. In either case, it will be intercepted by
one of Nyusha's friends.
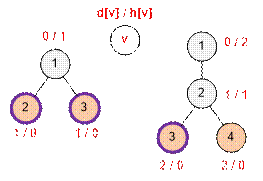
In
the second example (shown in the right diagram), one friend is enough, who can
be placed at either of the two exits – vertex 3 or 4. The butterfly will fly
from vertex 1 to vertex 2 in one minute. During that same time, the friend will
reach vertex 2 and catch the butterfly there.
Let
us consider the next example.
Nyusha
will need three friends to catch the butterfly.
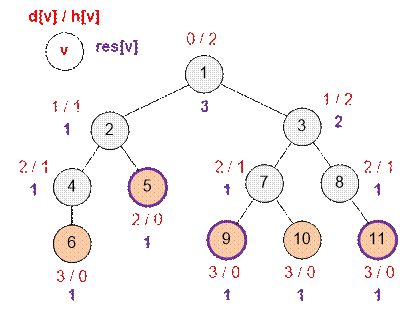
Algorithm implementation
Declare a constant for infinity and arrays.
#define INF 2000000000
vector<vector<int>
> g;
vector<int> d, h, res;
The
function dfs (v, p, cnt) performs a
depth-first search starting from vertex v and returns the value h[v].
Here, p is the parent of vertex v, and cnt is the distance
from vertex 1 to v. During the traversal, the values d[v] and h[v]
are computed for each vertex v.
int dfs(int v, int p = -1, int cnt = 0)
{
The
value cnt, which equals the distance from vertex 1 to v, is
stored in d[v].
d[v] = cnt;
int height = INF;
Iterate over all
the children of the vertex v. Consider the edge v → to. If to equals the parent of v (to = p), skip
it and move to the next child.
for (int to : g[v])
if (to !=
p)
In
the variable height compute the
value
min(h[to1],
h[to2], …, h[tok]),
where to1,
to2, …, tok are the children of vertex v.
height = min(height, dfs(to, v, cnt + 1));
If height = INF, then vertex
v is a leaf,
and set h[v]
= 0. Otherwise rerturn
h[v]
= 1 + min(h[to1], h[to2], …, h[tok])
return h[v] =
(height == INF) ? 0 : 1 + height;
}
The function dfs2 (v, p) performs a depth-first search
starting from vertex v and returns the value res[v]. Here, p
is the parent of vertex v.
int dfs2(int v, int p = -1)
{
int s = 0;
Let to1,
to2, …, tok be the children of vertex v. In the variable s, compute the sum:
res[to1]
+ res[to2] + … + res[tok]
for (int to : g[v])
if (to != p)
{
dfs2(to, v);
s += res[to];
}
If h[v] ≤ d[v], then one friend is sufficient, and res[v] = 1. Otherwise
res[v]
= res[to1] + res[to2] + … + res[tok] = s
return res[v] = (h[v] <=
d[v]) ? 1 : s;
}
The main
part of the program. Read the input data. Construct a graph.
scanf("%d", &n);
g.resize(n + 1);
for (i = 0; i < n - 1; i++)
{
scanf("%d %d", &a, &b);
g[a].push_back(b);
g[b].push_back(a);
}
Initialize
the arrays.
d.resize(n + 1);
h.resize(n + 1);
res.resize(n + 1);
Run two
depth-first searches. The first traversal computes the values of d[v]
and h[v] for each vertex v.
dfs(1);
dfs2(1);
Print the
answer – the minimum number of friends needed to catch the butterfly.
printf("%lld\n", res[1]);