11059. В поход!
В стране Смешариков – новый сезон! Теперь все герои отправляются в поход. Для
этого им необходимо встретиться в одной точке, а уже оттуда двинуться покорять
мир. Лосяш, координирующий действия Смешариков, знает координаты всех
участников похода. Помогите ему определить, какое минимальное количество секунд
потребуется, чтобы все Смешарики собрались вместе.
Изначально каждый Смешарик
находится в узле целочисленной сетки. Если Смешарик стоит в точке (x, y), то за
одну секунду он может переместиться в одну из точек (x, y + 1), (x + 1, y),
(x – 1, y), (x, y – 1) или остаться на месте.
Вход. В первой строке задано одно целое число
n (1 ≤ n ≤ 200000)
– количество Смешариков. В
следующих n строках указаны их начальные позиции. Каждая
позиция задаётся двумя целыми числами xi и yi (-1018
≤ xi, yi ≤ 1018).
Выход. Выведите минимальное количество секунд, необходимое для того, чтобы все
Смешарики собрались в одной точке.
|
Пример
входа 1 |
Пример
выхода 1 |
|
1 1 1 |
1 |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
|
2 1 3 4 4 |
2 |
|
|
|
|
Пример
входа 3 |
Пример
выхода 3 |
|
3 0 0 3 3 0 3 |
3 |
РЕШЕНИЕ
геометрия
– преобразование координат
Анализ
алгоритма
Пусть Смешарик находится в точке
(x, y). Тогда за t секунд он сможет оказаться в любой целочисленной точке ромба, как показано на рисунке.
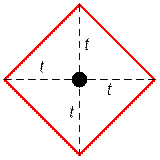
Нужно
найти наименьшее натуральное t, при котором все ромбы соответствующего
размера для каждого Смешарика будут иметь хотя бы одну общую целочисленную
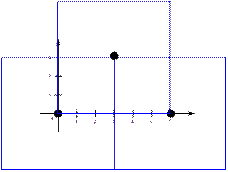
точку. Рассмотрим третий тест и изобразим ромбы для трёх Смешариков при t
= 1, 2, 3.
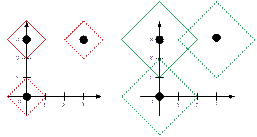
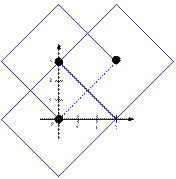
При t = 3 смешарики, например, могут встретиться в точке (0, 3) или (1,
2).
Повернем систему координат на -45° относительно начала
координат. При таком преобразовании
ромбы перейдут в квадраты. Выведем формулы поворота:
![]()
Или в декартовых координатах:
x’
+ iy’ = (x + iy) 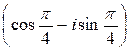
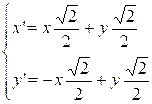
Избавимся от иррациональности, растянув изображение
в ![]() раз. Для этого воспользуемся
следующим преобразованием:
раз. Для этого воспользуемся
следующим преобразованием:
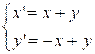
Преобразуем наши три точки:
·
(0, 0) → (0, 0)
·
(0, 3) → (3, 3)
·
(3, 3) → (6, 0)
Найдем координаты прямоугольника,
содержащего все точки (xi’, yi’) –
преобразованные начальные координаты смешариков. Обозначим:
·
minx = min (xi’); maxx
= max (xi’);
·
miny = min (yi’); maxy
= max (yi’);
Тогда прямоугольник с
противоположными углами (minx, miny) и (maxx,
maxy) содержит все точки (xi’, yi’).
При этом он является минимальным по площади прямоугольником, стороны которого
параллельны осям координат.
В нашем примере таким
прямоугольником будет (0, 0) – (6, 3).
Точкой
сбора смешариков (resx,
resy) будет центр
этого прямоугольника, то есть точка с координатами
(resx, resy) = 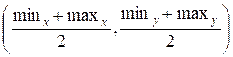
Теперь
нужно найти минимальное время, за которое все Смешарики смогут добраться из
своих точек (xi’,
yi’) в точку (resx,
resy). Для
повернутого ромба (квадрата в новой системе координат) расстояние от точки (xi’,
yi’) до (resx,
resy) вычисляется по
формуле:
max( | xi’ – resx |, | yi’ – resy |)
Таким
образом, все Смешарики смогут собраться в точке (resx, resy) за
время, равное максимальному из этих расстояний:
![]()
Реализация алгоритма
Объявим константу бесконечность INFL.
typedef long long ll;
#define INFL (ll)4e18
Входные
точки будем хранить в массиве inp.
vector<pair<ll, ll>> inp;
Функция
calc вычисляет расстояние от точки (x, y) до самого
удалённого смешарика. Преобразованные координаты смешариков находятся в массиве
inp.
ll calc(ll x, ll y)
{
ll res = 0;
for (auto p : inp)
res = max(res, max(abs(p.first - x), abs(p.second
- y)));
return res;
}
Основная
часть программы. Читаем входные данные.
cin >> n;
minx = INFL; maxx = -INFL; miny = INFL; maxy = -INFL;
for (i = 0; i < n; i++)
{
Читаем
исходные координаты смешарика (x, y). Выполняем поворот
координатной плоскости на -45° и
сохраняем полученные координаты в массиве inp.
cin >> x >> y;
nx = x + y;
ny = -x + y;
inp.push_back({ nx, ny });
После этого находим координаты
прямоугольника с противоположными углами (minx, miny)
и (maxx, maxy), который содержит все точки (xi’,
yi’) – преобразованные координаты смешариков.
minx = min(minx, nx);
maxx = max(maxx, nx);
miny = min(miny, ny);
maxy = max(maxy, ny);
}
Определяем точку сбора
смешариков (resx,
resy) – центр прямоугольника.
resx = (minx + maxx) / 2;
resy = (miny + maxy) / 2;
Вычисляем и выводим минимальное
время, необходимое для того, чтобы все смешарики смогли добраться из своих точек (xi’, yi’) до точки (resx, resy).
ans = calc(resx, resy);
cout << ans << "\n";