11059. On a hike!

In the land of Smeshariki, a new season has begun! Now all the heroes are setting out on a journey. To do this, they need to gather at a single point, and from there continue their quest to conquer the world. Losyash, who coordinates the actions of the Smeshariki, knows the coordinates of all the participants. Help him determine the minimum number of seconds required for all the Smeshariki to gather together.

Initially, each Smesharik is located at a node of the integer grid. If a Smesharik is at point (x, y), then in one second they can move to one of the points (x, y + 1), (x + 1, y), (x – 1, y), (x, y – 1), or remain at (x, y).

Input. The first line contains a single integer n (1 ≤ n ≤ 200000) – the number of Smeshariki. The next n lines specify their initial positions. Each position is given by two integers x_i and y_i (-10¹⁸ ≤ x_i, y_i ≤ 10¹⁸).

Output. Print the minimum number of seconds required for all the Smeshariki to gather at a single point.

Sample input 1	Sample output 1
1 1 1	1
Sample input 2	Sample output 2
2 1 3 4 4	2
Sample input 3	Sample output 3
3 0 0 3 3 0 3	3

SOLUTION

geometry – coordinates transformation

Algorithm analysis

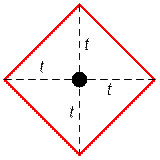
Let a Smesharik be at the point (x, y). Then in t seconds, it can reach any integer point inside the diamond, as shown in the figure.

It is required to find the smallest positive integer t such that the diamonds of the corresponding size for each Smesharik will all have at least one common integer point. Let us consider the third test and illustrate the diamonds for the three Smeshariks at t = 1, 2, 3.

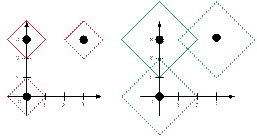
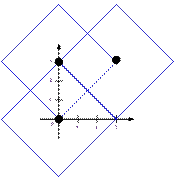
For t = 3, the Smeshariks can, for example, meet at the point (0, 3) or (1, 2).

Let us rotate the coordinate system by -45° relative to the origin. Under this transformation, the diamonds will turn into squares. Let us write down the rotation formulas:

Or, in Cartesian coordinates:

x’ + iy’ = (x + iy)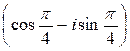

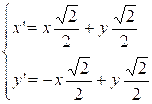
Let us eliminate the irrationality by stretching the image by a factor of . To do this, we use the following transformation:

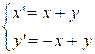
Now let us transform our three points:

· (0, 0) → (0, 0)

· (0, 3) → (3, 3)

· (3, 3) → (6, 0)

Let us find the coordinates of the rectangle containing all the points (x_i’, y_i’) – the transformed initial coordinates of the Smeshariks. Denote:

· min_x = min (x_i’); max_x = max (x_i’);

· min_y = min (y_i’); max_y = max (y_i’);

Then the rectangle with opposite corners (min_x, min_y) and (max_x, max_y) contains all the points (x_i’, y_i’). Moreover, it is the minimum area rectangle whose sides are parallel to the coordinate axes.

In our example, such a rectangle is (0, 0) – (6, 3).

The meeting point of the Smeshariks (res_x, res_y) will be the center of this rectangle, that is, the point with coordinates

(res_x, res_y) =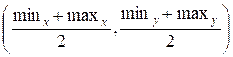

Now we need to find the minimum time in which all the Smeshariks can reach the point (res_x, res_y) from their positions (x_i’, y_i’). For the rotated diamond (a square in the new coordinate system), the distance from the point (x_i’, y_i’) to (res_x, res_y) is calculated using the formula:

max( | x_i’ – res_x |, | y_i’ – res_y |)

Thus, all the Smeshariks will be able to gather at the point (res_x, res_y) in a time equal to the maximum of these distances:

Algorithm implementation

Let us define the constant infinity INFL.

typedef long long ll;

#define INFL (ll)4e18

Store the input points in the array inp.

vector<pair<ll, ll>> inp;

The function calc computes the distance from the point (x, y) to the farthest Smesharik. The transformed coordinates of the Smeshariks are stored in the array inp.

ll calc(ll x, ll y)

{

ll res = 0;

for (auto p : inp)

res = max(res, max(abs(p.first - x), abs(p.second - y)));

return res;

}

The main part of the program. Read the input data.

cin >> n;

minx = INFL; maxx = -INFL; miny = INFL; maxy = -INFL;

for (i = 0; i < n; i++)

{

Read the initial coordinates of the Smesharik (x, y). Perform a -45° rotation of the coordinate plane and store the resulting coordinates in the array inp.

cin >> x >> y;

nx = x + y;

ny = -x + y;

inp.push_back({ nx, ny });

After that, find the coordinates of the rectangle with opposite corners (min_x, min_y) and (max_x, max_y), which contains all the points (x_i’, y_i’) – the transformed coordinates of the Smeshariks.

minx = min(minx, nx);

maxx = max(maxx, nx);

miny = min(miny, ny);

maxy = max(maxy, ny);

}

Determine the meeting point of the Smeshariks (res_x, res_y) – the center of the rectangle.

resx = (minx + maxx) / 2;

resy = (miny + maxy) / 2;

Compute and print the minimum time required for all the Smeshariks to reach the point (res_x, res_y) from their positions (x_i’, y_i’).

ans = calc(resx, resy);

cout << ans << "\n";