11196. Еще
больше странных фотографий (Бронза)
Фермер Джон фотографирует n своих
коров.
Каждая корова имеет целое число –
“ID породы” в интервале 1 .. 100. ФД хочет разбить всех коров на несвязные группы
(другими словами, поместить каждую корову ровно в одну группу) и затем
выставить группы так, чтобы сумма “ID породы” коров в первой группе была чётной, во второй – нечётной и так далее, чередуя чётные и нечётные.
Какое максимальное количество
групп может сформировать ФД?
Вход. Первая строка содержит число n
(2 ≤ n ≤ 1000). Следующая строка содержит n целых
чисел, представляющих “ID породы”.
Выход. Выведите максимально возможное количество групп на фото ФД. Можно доказать,
что хотя бы одна группа будет всегда.
|
Пример
входа 1 |
Пример
выхода 1 |
|
7 1 3 5 7 9 11 13 |
3 |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
|
7 11 2 17 13 1 15 3 |
5 |
РЕШЕНИЕ
жадные алгоритмы
Анализ алгоритма
Подсчитаем
количество четных even и нечетных odd чисел. Если количество нечетных
чисел больше четных, то из каждой пары нечетных чисел можно сделать группу с
четной суммой.
Сумма “ID породы” коров в первой группе была
чётной, во второй – нечётной и так далее. Для максимизации
числа групп мы можем сформировать групп с четной суммой на 1 больше чем с нечетной.
![]()
Если
количество четных групп even больше odd + 1, то используем odd + 1 четных групп, а коров из остальных групп с четной суммой
присоединяем к одной из использованных четных групп.
Пример
Рассмотрим первый пример. Он
содержит odd = 7 нечетных и even = 0 четных чисел. Пока odd > even, из двух нечетных чисел делаем
группу с четной суммой.
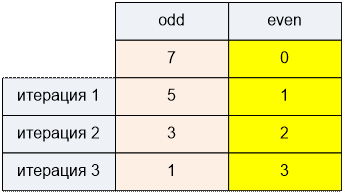
Три раза из двух нечетных чисел
сделали три группы с четной суммой. Например, мы можем составить следующие
группы:

Групп с нечетной суммой у нас 1,
следовательно будет задействовано только 2 группы с четной суммой. Оставшиеся
группы коров с четной суммой можно присоединить к одной из задействованных
групп коров с четной суммой.
Далее приведен один из способов
сформировать 3 группы (коровы 9 и 11 присоединены к группе с коровами 5 и 7):

Во втором примере один из
способов сформировать 5 групп выглядит так:
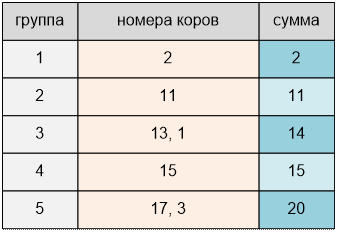
Реализация алгоритма
Читаем
количество коров n.
scanf("%d", &n);
Подсчитываем
количество четных even и нечетных odd “ID пород”.
odd = even
= 0;
Читаем
и обрабатываем информацию про n коров.
for (i = 0; i < n; i++)
{
scanf("%d", &x);
if (x % 2 == 0) even++; else odd++;
}
Пока odd
> even, из двух нечетных чисел делаем группу с четной суммой.
while (odd > even)
{
odd = odd - 2;
even++;
}
Число
четных групп even может быть не больше чем odd + 1.
if (even > odd + 1) even = odd + 1;
Выводим
максимально возможное сформированное количество групп.
printf("%d", even + odd);
Python реализация
Читаем
количество коров n.
n = int(input())
Подсчитываем
количество четных even и нечетных odd “ID пород”.
odd = even = 0
Читаем список “ID пород”.
lst = list(map(int,input().split()))
Читаем
и обрабатываем информацию про n коров.
for x in lst:
if x % 2 == 0:
even += 1
else:
odd += 1
Пока odd
> even, из двух нечетных чисел делаем группу с четной суммой.
while odd > even:
odd -= 2
even += 1
Число
четных групп even может быть не больше чем odd + 1.
if even > odd + 1:
even = odd + 1
Выводим
максимально возможное сформированное количество групп.
print(even + odd)