11245. Разбиение
на палиндромы
Разделение строки называется палиндромным
разбиением, если каждая подстрока в этом разбиении является палиндромом.
Например, строка “ababbbabbababa” может быть разделена как “aba|b|bbabb|a|b|aba”
– это пример палиндромного разбиения.
Определите наименьшее количество
разрезов, необходимых для палиндромного разбиения заданной строки. Например:
·
для строки “ababbbabbababa” требуется минимум 3 разреза,
которые образуют разбиение “a|babbbab|b|ababa”;
·
если строка уже является палиндромом, то потребуется 0 разрезов;
·
если все символы строки длины n различны, то минимальное количество
разрезов равно n – 1.
Вход. Одна строка s длины
не более 1000 символов.
Выход. Выведите минимальное количество
разрезов, необходимых для палиндромного разбиения строки s.
|
Пример
входа 1 |
Пример
выхода 1 |
|
abbaazxzazbxbz |
2 |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
|
abccba |
0 |
|
|
|
|
Пример
входа 3 |
Пример
выхода 3 |
|
qwerty |
5 |
РЕШЕНИЕ
динамическое
программирование
Анализ алгоритма
Пусть s – входная строка. Подстрока si … sj является палиндромом, если выполняется одно из следующих условий:
·
i ≥ j (подстрока пустая или состоит из одного
символа);
·
si = sj и подстрока si+1…sj-1 является
палиндромом;
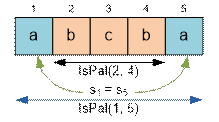
Пусть функция
IsPal(i, j) возвращает 1, если si…sj является палиндромом, и 0 в противном случае. Значения IsPal(i, j) сохраняем в ячейках
pal[i][j].
Пусть функция f(i, j)
возвращает минимальное
количество разрезов, необходимых для палиндромного разбиения строки si…sj.
Значения
этой функции будем сохранять в ячейках массива dp[i][j]. Тогда ответом на задачу будет значение f(0, s.size() – 1).
Отметим,
что f(i, i) = 0, так как строка
из одной буквы уже является палиндромом.
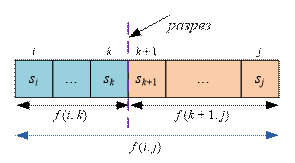
Для вычисления f(i, j) разрежем подстроку si…sj
на две части: si…sk и sk+1…sj
(i ≤ k < j). Рекурсивно решаем задачи на строках si…sk
и sk+1…sj. Ищем такое значение k (i ≤ k < j), для которого сумма f(i, k) + f(k
+ 1, j) + 1 будет минимальной. Слагаемое 1 в сумме означает, что мы
совершаем один разрез между символами sk
и sk+1. Таким
образом, получаем
следующее рекуррентное соотношение:
f(i, j) = ![]()
Пример
Например, для
строки “ababccb”
из
7 символов имеем:
f(1, 7) = ![]()
Сумма принимает наименьшее
значения при k = 3:
f(1, 7) = f(1, 3) + f(4, 7) + 1 = 0 + 0 + 1 = 1
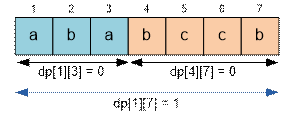
Так как строки “aba” и “bccb” являются
палиндромами, то f(1, 3) = f(4, 7) = 0.
Реализация алгоритма
Объявим константы, входную строку s и рабочие
массивы.
#define MAX 1001
#define INF 0x3F3F3F3F
int dp[MAX][MAX], pal[MAX][MAX];
string s;
Функция IsPal(i, j)
проверяет, является ли подстрока si…sj палиндромом. Подстрока si … sj является палиндромом, если si = sj
и si+1…sj-1 является
палиндромом. Значения IsPal(i, j) сохраняем в ячейках массива pal[i][j].
int IsPal(int i, int j)
{
if (i >= j) return pal[i][j] = 1;
if
(pal[i][j] !=
-1) return pal[i][j];
return pal[i][j] =
(s[i] ==
s[j])
&& IsPal(i + 1, j - 1);
}
Функция f(i, j) возвращает минимальное количество разрезов,
необходимых для палиндромного разбиения подстроки si…sj.
int f(int i, int j)
{
Если i = j, подстрока si…sj состоит из одного символа, и резать её нет смысла.
Если i > j, подстрока si…sj считается пустой, и разрезы также не
требуются.
if (i >= j) return 0;
Если значение f(i, j)
уже было
вычислено ранее, возвращаем сохранённое значение из массива dp[i][j].
if
(dp[i][j] !=
INF) return dp[i][j];
Если подстрока si…sj (i < j) является
палиндромом, то резать ее смысла нет. В этом случае минимальное количество разрезов равно
0.
if
(IsPal(i, j)) return dp[i][j] = 0;
Разрежем подстроку
si…sj на две части: si…sk (i ≤ k) и sk+1…sj (k + 1 ≤ j). Далее рекурсивно
решаем задачи для обеих частей: si…sk и sk+1…sj.
Ищем такое значение k (i ≤ k < j), для которого сумма f(i, k) + f(k
+ 1, j) + 1 наименьшая.
for (int k = i; k
< j; k++)
dp[i][j] = min(dp[i][j], f(i, k)
+ f(k + 1, j) + 1);
Возвращаем ответ dp[i][j] = f(i, j).
return dp[i][j];
}
Основная часть программы. Читаем входную строку.
cin >> s;
Инициализируем массивы.
memset(dp,
0x3F, sizeof(dp));
memset(pal,
-1, sizeof(pal));
Вычисляем и выводим ответ.
res
= f(0, s.size() - 1);
cout
<< res << endl;