11245. Palindrome partitioning
A string partition is called a palindromic
partition if every substring in this partition is a palindrome.
For example, the string “ababbbabbababa” can be partitioned as “aba|b|bbabb|a|b|aba”
– this is an example of a palindromic partition.
Determine the minimum number of cuts
required for the palindromic partitioning of a given string. For example:
·
for
the string “ababbbabbababa” a minimum of 3 cuts are needed to
create the partition “a∣babbbab∣b∣ababa”;
·
if the
string is already a palindrome, 0 cuts are needed;
·
if all
the characters of a string of length n are different, the
minimum number of cuts required is n – 1.
Input. One string s of length no more than 1000.
Output. Print
the minimum number of cuts needed for the palindromic partitioning of the
string s.
|
Sample
input 1 |
Sample
output 1 |
|
abbaazxzazbxbz |
2 |
|
|
|
|
Sample
input 2 |
Sample
output 2 |
|
abccba |
0 |
|
|
|
|
Sample
input 3 |
Sample
output 3 |
|
qwerty |
5 |
SOLUTION
dynamic programming
Algorithm analysis
Let s be the input
string. The substring si … sj is a palindrome if
one of the following conditions is satisfied:
·
i ≥ j (the substring is empty or consists of
a single character);
·
si = sj and the substring si+1…sj-1 is a palindrome;
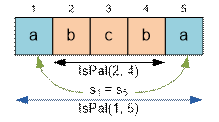
Let the function IsPal(i, j) return 1 if the substring
si…sj is a palindrome,
and 0 otherwise. The values of IsPal(i, j) are stored in the cells
pal[i][j].
Let the function f(i, j)
return the minimum number of cuts required to partition the substring si…sj into palindromes. The values of this function will be
stored in the cells of the array dp[i][j]. Therefore, the solution to the problem
will be f(0, s.size() – 1).
Note that f(i, i) = 0, as a string consisting of a
single character is already a palindrome.
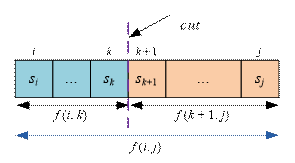
To compute f(i, j), cut the substring si…sj
into two
parts: si…sk and sk+1…sj (i ≤ k < j). Recursively solve the problems on the strings si…sk
and sk+1…sj. Look for the value of k (i ≤ k < j) that minimizes the sum f(i, k) + f(k + 1, j) + 1. The term +1 in the sum
represents the single cut made between the characters sk and sk+1. Thus, we obtain the following
recurrence relation:
f(i, j) = ![]()
Example
For example, for the
string “ababccb” consisting of 7 characters, we have:
f(1, 7) = ![]()
The sum takes its minimum value at k = 3:
f(1, 7) = f(1, 3) + f(4, 7) + 1 = 0 + 0 + 1 = 1
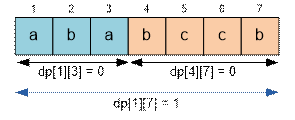
Since the substrings “aba” and “bccb” are palindromes, f(1, 3) = f(4, 7) = 0.
Algorithm implementation
Define the constants, the input string s, and the arrays.
#define MAX 1001
#define INF 0x3F3F3F3F
int dp[MAX][MAX], pal[MAX][MAX];
string s;
The function IsPal(i, j)
checks
whether the substring si…sj is a palindrome. The substring si …
sj is a palindrome if si = sj and si+1…sj-1 is a palindrome. The values of IsPal(i, j)
are stored in
the cells of the array pal[i][j].
int IsPal(int i, int j)
{
if (i >= j) return pal[i][j] = 1;
if
(pal[i][j] !=
-1) return pal[i][j];
return pal[i][j] =
(s[i] ==
s[j])
&& IsPal(i + 1, j - 1);
}
The function f(i, j) returns the minimum number of cuts
required to partition the substring si…sj into palindromes.
int f(int i, int j)
{
If i = j, the substring si…sj consists of a single character, and
no cuts are needed.
If i > j, the substring si…sj
is considered
empty, and no cuts are required.
if (i >= j) return 0;
If the value f(i, j)
is already computed,
return the stored value from the dp[i][j].
if
(dp[i][j] !=
INF) return dp[i][j];
If the substring si…sj (i < j) is a palindrome, there is
no need to make any cuts. In this case, the minimum number of cuts is 0.
if
(IsPal(i, j)) return dp[i][j] = 0;
Cut the substring si…sj
into two
parts: si…sk (i ≤ k) and sk+1…sj (k + 1 ≤ j). Then, recursively solve the problems for both parts: si…sk
and sk+1…sj. Find the value of k (i ≤ k < j) for which the sum f(i, k) + f(k
+ 1, j) + 1 is minimized.
for (int k = i; k
< j; k++)
dp[i][j] = min(dp[i][j], f(i, k)
+ f(k + 1, j) + 1);
Return the answer dp[i][j] = f(i, j).
return dp[i][j];
}
The
main part of the program. Read the input string.
cin >> s;
Initialize
the arrays.
memset(dp,
0x3F, sizeof(dp));
memset(pal,
-1, sizeof(pal));
Compute
and print the answer.
res
= f(0, s.size() - 1);
cout
<< res << endl;