11247. Контейнер с наибольшим количеством воды

Имеется массив h целых чисел длины n, задающий высоты n вертикальных линий. Для каждой i-й линии её конечные точки заданы координатами (i, 0) и (i, h_i).

Найдите две такие линии, которые вместе с осью x образуют контейнер, способный удержать максимальное количество воды.

Вход. Первая строка содержит размер n (n ≤ 10⁵) массива h. Вторая строка содержит n целых чисел – элементы массива h, каждое из которых не превышает 10⁹.

Выход. Выведите максимальный объём воды, который может удержать контейнер.

Пример входа	Пример выхода
9 1 8 6 2 5 4 8 3 7	49

РЕШЕНИЕ

два указателя

Анализ алгоритма

Сначала вычислим объем воды в контейнере между крайними верткальными линиями, то есть между линиями пары (l, r) = (1, n). Затем будем двигать указатели l и r навстречу друг другу:

· если h_l < h_r, то увеличим l на 1;

· если h_l ≥ h_r, то уменьшим r на 1;

Объем воды между линиями l и r равен min(h_l, h_r) * (r – l). Среди всех полученных значений находим наибольшее.

Задачу можно решить за O(n²). Однако из-за ограничения n ≤ 10⁵ такое решение приведёт к превышению лимита времени (Time Limit). Достаточно перебрать пары линий (i, j), для которых 1 ≤ i < j ≤ n, и далее для каждой такой пары вычислить объем воды, который они могут удерживать. Среди всех вычисленных значений находим максимальный объём.

Пример

Контейнер из первого теста имеет вид:

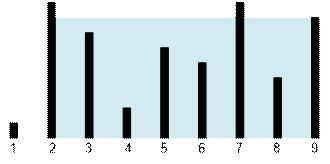
Наибольшее количество воды можно удержать между линиями 2 и 9. Высота уровня воды составит 7, а объем воды равен 7 * 7 = 49.

Реализация алгоритма

Читаем входные данные.

scanf("%d", &n);

h.resize(n);

for (i = 0; i < n; i++)

scanf("%lld", &h[i]);

В переменной res будем хранить максимальное количество воды, которое может удерживать контейнер.

long long res = 0;

Инициализируем пару указателей (l, r) = (1, n).

int l = 0, r = h.size() - 1;

Двигаем указатели l и r навстречу друг другу, пока они не встретятся.

while (l < r)

{

Объем воды между линиями l и r равен min(h_l, h_r) * (r – l). Среди всех таких объемов находим максимальный.

res = max(res, min(h[l], h[r]) * (r - l));

Перемещаем указатели.

if (h[l] < h[r])

l += 1;

else

r -= 1;

}

Выводим ответ.

printf("%lld\n", res);

Реализация алгоритма – O(n²), Time Limit

Читаем входные данные.

scanf("%d", &n);

v.resize(n);

for (i = 0; i < n; i++)

scanf("%lld", &v[i]);

В переменной res будем хранить максимальное количество воды, которое может удерживать контейнер.

long long res = 0;

Перебираем все возможные пары линий (i, j), 1 ≤ i < j ≤ n.

for (i = 0; i < n; i++)

for (j = i + 1; j < n; j++)

Объем воды между линиями i и j равен min(v_i, v_j) * (j – i). Среди всех таких объемов находим максимальный.

res = max(res, min(v[i], v[j]) * (j - i));

Выводим ответ.

printf("%lld\n", res);