11247. Container with most water

There is an array h of integers of length n, representing the heights of n vertical lines. For each i-th line, its endpoints are defined by the coordinates (i, 0) and (i, h_i).

Find two lines that, together with the x-axis, form a container capable of holding the maximum amount of water.

Input. The first line contains the size n (n ≤ 10⁵) of the array h. The second line contains n positive integers, the elements of the array h, each of which does not exceed 10⁹.

Output. Print the maximum volume of water that the container can hold.

Sample input	Sample output
9 1 8 6 2 5 4 8 3 7	49

SOLUTION

two pointers

Algorithm analysis

First, compute the volume of water in the container formed by the outermost vertical lines, i.e., between the lines of the pair (l, r) = (1, n). Then, move the pointers l and r towards each other:

· if h_l < h_r, increase l by 1;

· if h_l ≥ h_r, decrease r by 1;

The volume of water between the lines l and r is equal to min(h_l, h_r) * (r – l). Among all the calculated values, find the maximum.

The problem can be solved in O(n²). However, due to the constraint n ≤ 10⁵, such a solution would result in a time limit exceeded (TLE). It is sufficient to iterate over the pairs of lines (i, j), where 1 ≤ i < j ≤ n, and for each such pair, calculate the volume of water they can hold. Among all the computed values, find the maximum volume.

Example

The container from the first test looks like this:

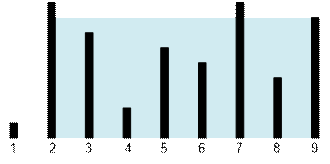
The maximum amount of water can be held between the lines 2 and 9. The water level height is 7, and the volume of water is 7 * 7 = 49.

Algorithm realization

Read the input data.

scanf("%d", &n);

h.resize(n);

for (i = 0; i < n; i++)

scanf("%lld", &h[i]);

Store the maximum amount of water the container can hold in the variable res.

long long res = 0;

Initialize two pointers (l, r) = (1, n).

int l = 0, r = h.size() - 1;

Move the pointers l and r towards each other until they meet.

while (l < r)

{

The volume of water between the lines l and r is equal to min(h_l, h_r) * (r – l). Among all such volumes, find the maximum.

res = max(res, min(h[l], h[r]) * (r - l));

Move the pointers.

if (h[l] < h[r])

l += 1;

else

r -= 1;

}

Print the answer.

printf("%lld\n", res);

Algorithm realization – O(n²), Time Limit

Read the input data.

scanf("%d", &n);

v.resize(n);

for (i = 0; i < n; i++)

scanf("%lld", &v[i]);

Store the maximum amount of water the container can hold in the variable res.

long long res = 0;

Iterate over all possible pairs of lines (i, j), where 1 ≤ i < j ≤ n.

for (i = 0; i < n; i++)

for (j = i + 1; j < n; j++)

The volume of water between the lines l and r is equal to min(v_i, v_j) * (j – i). Among all such volumes, find the maximum.

res = max(res, min(v[i], v[j]) * (j - i));

Print the answer.

printf("%lld\n", res);