11261. Cutting a stick
You need to cut a wooden stick into pieces.
The most affordable company, The Analog Cutting
Machinery, Inc. (ACM), charges money based on the length of the stick being cut.
Their procedure requires making only one cut at a time.
It is easy to see that different choices of
the cutting order lead to
different costs. For example, consider a stick of length
10 meters that needs to be cut at 2, 4, and 7 meters from one end. Consider a
few options:
·
You
could cut first at 2 meters, then at 4 meters, and finally at 7 meters. This
would result in a cost of 10 + 8 + 6 = 24, because the first piece was 10
meters, the second 8 meters, and the third 6 meters.
·
In
another option, if you first cut at 4 meters, then at 2 meters, and finally at
7 meters, the cost would be 10 + 4 + 6 = 20, which is the better price.
Your boss trusts your computing skills to
determine the minimal cost of cutting the given stick.
Input. Consist of several test cases. The first line of each
test case contains the length of the stick l (l < 1000)
that needs to be cut. The next line contains the number of
cuts n (n < 50) to be made.
The following line contains n positive
integers ci (0 < ci <
l), representing the
positions for the cuts, given in strictly increasing order. A line with l = 0 denotes the end of the input data.
Output. Print the minimal cost of cutting the stick in the
format given in the example.
|
Sample
input |
Sample
output |
|
100 3 25 50 75 10 4 4 5 7 8 0 |
The minimum cutting is 200. The minimum cutting is 22. |
SOLUTION
dynamic
programming
Algorithm analysis
Let the array m
contain the cutting points: m1, …, mn. Add the start and end points: m0 = 0 and mn+1 = l.
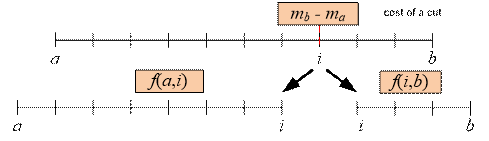
Let the function f(a, b)
return the minimal cost of cutting a stick from ma
to mb considering the necessary
cutting points within the segment. There are no cutting points within
the segment [ma; ma + 1], so f(a,
a + 1) = 0. The solution to the problem will be
the value of f(0, n + 1). Store the computed values
of f(a, b)
in the cells
of the array dp[a][b].
Let the segment of the
stick [ma, mb] be cut into several pieces. If the
first cut is made at point mi (a < i < b) , the cost of the cut
itself will be mb – ma. Then, the remaining
pieces need
to be cut at the costs f(a, i) and f(i, b), respectively. Choose i to
minimize the total cost:
f(a, b)
= ![]() + mb – ma
+ mb – ma
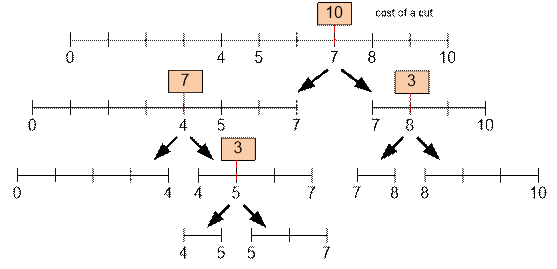
Example
Consider the second test case. Here is one
possible way
to cut
a stick of length 10 with a cost of 10 + 7 + 3 + 3 = 23:
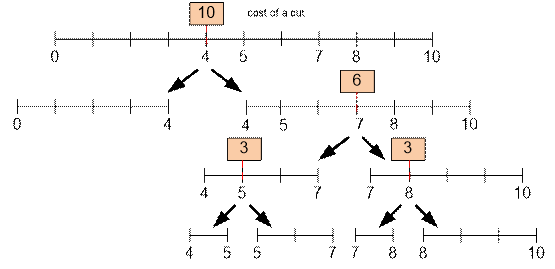
Now, consider the
optimal way
to cut the stick, which has
a cost of 10 + 6 + 3 + 3 =
22:
Algorithm implementation
Declare constants
and arrays.
#define MAX 55
#define INF 0x3F3F3F3F
int dp[MAX][MAX];
int m[MAX];
The function f(a, b) returns the minimum
cost of cutting a piece of stick on the segment [a; b] at the cutting
points located inside the segment.
int f(int
a, int b)
{
If a + 1 = b, then there are no cutting points
within the segment [a; b]. Return 0.
if (b - a == 1) return 0;
If the value of f(a, b) is already computed, return it.
if (dp[a][b] !=
INF) return dp[a][b];
Make a cut at the point i (a < i < b). Compute the cost as follows:
f(a, b)
= ![]() + mb – ma
+ mb – ma
for (int i = a + 1; i
< b; i++)
dp[a][b] = min(dp[a][b], m[b] - m[a] + f(a, i) +
f(i, b));
Return the result f(a, b) = dp[a][b].
return
dp[a][b];
}
The main part of the program. Read the input data for each test case.
while (scanf("%d",&l),l)
{
scanf("%d",&n);
Add the start and end cutting points: m0
= 0, mn+1 = l.
m[0] = 0; m[n+1] = l;
for (i = 1; i <=
n; i++)
scanf("%d",&m[i]);
Initialize the dp array.
memset(dp,0x3F,sizeof(dp));
Find and print the answer.
printf("The
minimum cutting is %d.\n",f(0,n+1));
}