11270. Неисчислимые пути

Задан прямоугольник размером n * m. Прямоугольник размером a * b отрезается от правого верхнего угла. Сколько способов имеется у муравья добраться из верхнего левого угла в нижний правый, если он может двигаться по линиям сетки только вправо или вниз.

Вход. Первая строка содержит количество тестов t. Каждая из следующих t строк содержит четыре целых числа n, m, a, b (2 ≤ n, m ≤ 400000, 1 ≤ a < n, 1 ≤ b < m).

Выход. Для каждого теста выведите в отдельной строке количество способов, которыми муравей может добраться до нижнего правого угла при заданных условиях. Ответ следует выводить по модулю 10⁹ + 7.

Пример входа	Пример выхода
3 2 2 1 1 4 5 2 2 7 7 6 6	5 105 50

РЕШЕНИЕ

комбинаторика

Анализ алгоритма

Рассмотрим целый (без вырезов) прямоугольник размером n * m. Вычислим количество путей от клетки (0, 0) до клетки (n, m). Поскольку путь между указанными точками имеет длину n + m, и при этом содержит m горизонтальных сегментов, то число путей равно ways(n, m) = . Если путь рассматривать как выбор n вертикальных сегментов из n + m, то число путей равно . Однако заметим, что эти значения равны так как = = .

Теперь рассмотрим прямоугольник размером n * m с вырезанным правым верхом размером a * b.

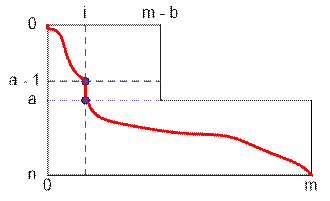
Путь из (0, 0) в (n, m) разобъем на три части:

· двигаемся из (0, 0) в (a – 1, i), где 0 ≤ i ≤ m – b;

· двигаемся из (a – 1, i) в (a, i);

· двигаемся из (a, i) в (n, m);

Количество путей из (0, 0) в (a – 1, i) равно ways(a – 1, i).

Количество путей из (a, i) в (n, m) равно ways(n – a, m – i).

Таким образом число путей из (0, 0) в (n, m) равно

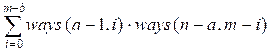
Пример

Рассмотрим прямоугольник 2 * 2, у которого вырезан правый верхний угол размером 1 * 1. У муравья имеется 5 способов добраться из верхнего левого угла в нижний правый.

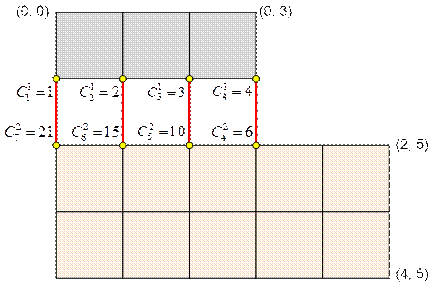
Рассмотрим второй пример. Из прямоугольника 4 * 5 вырезан правый верхний угол размером 2 * 2.

· Рассмотрим количество путей из (0, 0) в (1, i), 0 ≤ i ≤ 3.

· Рассмотрим количество путей из (2, i) в (4, 5), 0 ≤ i ≤ 3.

Количество путей из (0, 0) в (4, 5) равно

= =

+ + + =

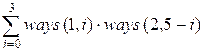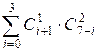1 * 21 + 2 * 15 + 3 * 10 + 4 * 6 = 21 + 30 + 30 + 24 = 105

Реализация алгоритма

Объявим константы.

#define MAX 1000001

#define MOD 1000000007

Объявим массивы: fact содержит факториалы чисел по модулю MOD, factinv содержит числа, обратные факториалам чисел по модулю MOD:

fact[n] = n! mod 1000000007

factinv[n] = n! ^-1 mod 1000000007

typedef long long ll;

ll fact[MAX], factinv[MAX];

Функция pow вычисляет степень числа по модулю: xⁿ mod p.

ll pow(ll x, ll n, ll p)

{

if (n == 0) return 1;

if (n % 2 == 0) return pow((x * x) % p, n / 2, p);

return (x * pow(x, n - 1, p)) % p;

}

Функция inverse находит число, обратоне x по простому модулю p. Поскольку число p простое, то по теореме Ферма x^p-1 mod p = 1 для всякого 1 ≤ x < p. Равенство можно переписать в виде (x * x^p-2) mod p = 1, откуда обратным к x является число x^p-2 mod p.

ll inverse(ll x, ll p)

{

return pow(x, p - 2, p);

}

Функция Cnk вычисляет биномиальный коэффициент по формуле:

=

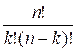
ll Cnk(int n, int k)

{

return ((fact[n] * factinv[k]) % MOD * factinv[n - k]) % MOD;

}

Функция ways вычисляет количество путей на решетке размером n * m от клетки (0, 0) до клетки (n, m). Поскольку путь между указанными точками имеет длину n + m, и при этом содержит m горизонтальных сегментов, то число путей равно .

ll ways(int n, int m)

{

return Cnk(n + m, m);

}

Основная часть программы. Заполняем массивы факториалов fact и factinv.

fact[0] = 1;

for (i = 1; i < MAX; i++)

fact[i] = (fact[i - 1] * i) % MOD;

factinv[0] = 1;

for (i = 1; i < MAX; i++)

factinv[i] = inverse(fact[i], MOD);

Читаем входные данные.

scanf("%d", &tests);

while (tests--)

{

scanf("%d %d %d %d", &n, &m, &a, &b);

В переменной res вычисляем ответ по формуле.

res = 0;

for (i = 0; i <= m - b; i++)

res = (res + ways(a - 1, i) * ways(n - a, m - i)) % MOD;

Выводим ответ.

printf("%lld\n", res);

}