11286. Twice bigger
Given a sorted array A of n integers.
For each index i, find the number of elements in the array that lie
between
Ai and 2 * Ai inclusive.
Input. The first line contains the size n (n ≤ 105)
of array A. The second line
contains n integers, each ranging from 0 to 109, in sorted order.
Output. Print n integers. For each index i (1 ≤ i ≤ n)
of the array, print the number
of elements lying between Ai
and 2 * Ài inclusive.
|
Sample
input |
Sample
output |
|
10 1 2 3 4 5 6 7 8 9
10 |
2 3 4 5 6 5 4 3 2
1 |
SOLUTION
two
pointers
Algorithm analysis
The interval A[i … j]
will be called good if
the numbers in it lie in the range [Ai; 2 * Ài] inclusive (meaning Aj ≤ 2 * Ài).
We implement
a sliding window using two pointers i and j and maintain it so that the current interval [i … j] is good,
while the interval [i … j + 1] is bad.
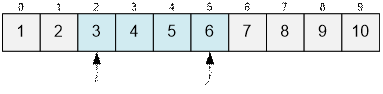
For example,
for the following sequence:
·
the intervals [2; 2], [2; 3], [2; 4], and [2; 5] are good.
·
the intervals [2; 6], [2; 7], … are bad.
If Aj ≤ 2 * Ài, extend the current interval to À[i …
j + 1].
Otherwise, reduce it to À[i + 1 … j]. Before moving the pointer i, print
the number of elements lying between Ai
and 2 * Ài
inclusive. It equals j – i.
The algorithm’s complexity is linear, i.e.
O(n).
Example
Let’s
consider the movement of pointers for the given example.

For the
given condition Aj ≤ 2 * Ài, so we move the pointer j forward.
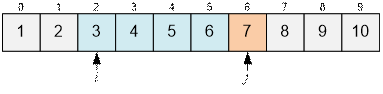
Now Aj > 2 * Ài. We need to move the pointer i forward. However, before
moving it, print the number of elements lying between Ai and 2 * Ài inclusive.
It is equal to j – i = 6 – 2 = 4.
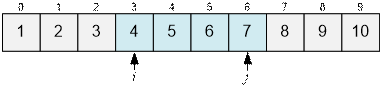
Move j forward until Aj ≤ 2 * Ài.
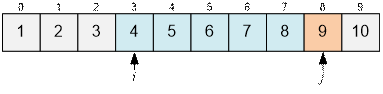
Now Aj > 2 * Ài. Print the answer for i = 3 (it equals j – i = 8 – 3 = 5) and increase i by
1.
Algorithm realization
Read the input
data.
scanf("%d", &n);
for (i = 0; i < n; i++)
scanf("%d", &a[i]);
Initialize the pointers i = j = 0.
i = j = 0;
Move the pointers forward until an answer is found for each
value of i < n.
while (i < n) // [i..j]
{
If Aj ≤ 2 * Ài (and j has
not exceeded the array bounds, meaning j < n), extend the current interval
by incrementing the pointer j.
if ((j
< n) && (a[j] <= 2 * a[i])) j++;
else
{
If Aj > 2 * Ài, print the answer
for index i and increment i by one.
printf("%d ", j - i);
i++;
}
}
Algorithm realization – binary search, O(n log n)
Read the input
data.
scanf("%d", &n);
v.resize(n);
for (i = 0; i < n; i++)
scanf("%d", &v[i]);
For each index i < n, using binary search, find the largest value
of the index x such that the numbers from Ài to 2 * Ài are
contained in the interval [i; x – 1], and Ax > 2 * Ài. The count
of numbers in the interval [i; x – 1] equals x – i.
for (i = 0; i < n; i++)
{
x = upper_bound(v.begin(), v.end(), 2 * v[i]) - v.begin();
printf("%d ", x - i);
}
Java realization
import java.util.*;
public class Main
{
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
int n = con.nextInt();
int m[] = new int[n];
for(int i = 0; i < n; i++)
m[i] = con.nextInt();
int i = 0, j = 0;
while (i < n) // [i..j]
{
if ((j < n)
&& (m[j] <= 2 * m[i])) j++;
else
{
System.out.print(j - i + "
");
i++;
}
}
con.close();
}
}
Python realization
Read the input
data.
n = int(input())
lst = list(map(int,input().split()))
Initialize the pointers i = j = 0.
i = j = 0
Move the pointers forward until an answer is found for each
value of i < n.
while (i < n): # [i..j]
If Aj ≤ 2 * Ài (and j has
not exceeded the array bounds, meaning j < n), extend the current interval
by incrementing the pointer j.
if (j < n and lst[j] <= 2 * lst[i]):
j += 1
else:
If Aj > 2 * Ài, print the answer
for index i and increment i by one.
print(j - i, end=" ");
i += 1
Python realization – binary
search, O(n log n)
from bisect import bisect_right
Read the input data.
n = int(input())
v = list(map(int, input().split()))
For each index i < n, using binary search, find the largest value
of the index x such that the numbers from Ài to 2 * Ài are
contained in the interval [i; x – 1], and Ax > 2 * Ài. The count
of numbers in the interval [i; x – 1] equals x – i.
for i in range(n):
x = bisect_right(v, 2 * v[i])
print(x - i, end=" ")