11289. Labelled graphs
Let the number of vertices in a graph
be n. Compute the number of labelled graphs with n vertices
(labelled means that the vertices are marked with the numbers from 1 to n).
The edges of the graphs are considered undirected, and loops and multiple edges
are forbidden.
Input. The number of vertices n (1 ≤ n
≤ 105) in the graph.
Output. Print the number of labelled graphs with n vertices.
Print the answer modulo 109 + 7.
|
Sample
input 1 |
Sample output
1 |
|
2 |
2 |
|
|
|
|
Sample
input 2 |
Sample output 2 |
|
3 |
8 |
SOLUTION
graphs
Algorithm analysis
In the graph with n
vertices p = n * (n – 1) / 2 edges can be drawn. By
choosing an arbitrary subset of edges, one can obtain a labelled graph. The
number of labelled graphs equals to the number of subsets of the entire set of
possible edges, namely 2p.
Example
For n = 2 there are 2 graphs. There
are no edges in the first graph. The second graph has a single edge.
![]()
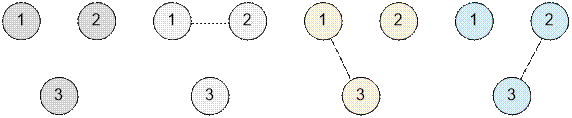
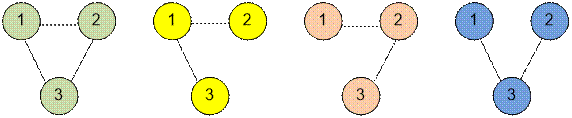
For n = 3 there are 8 graphs:
Algorithm realization
Function PowMod
computes xn mod m.
long long PowMod(long long x, long long n, long long m)
{
if (n == 0) return 1;
if (n % 2 == 0) return PowMod((x * x) % m, n / 2, m);
return (x * PowMod(x, n - 1, m)) % m;
}
The main
part of the program. Read the input value of n.
scanf("%lld", &n);
Find and
print the answer res = ![]() mod (109 + 7).
mod (109 + 7).
p = n * (n
- 1) / 2;
res =
PowMod(2, p, MOD);
printf("%lld\n", res);