11311. Расстояние до заданной точки

Это интерактивная задача

На плоскости отмечены целые точки с координатами, не превосходящими 10⁶. Движение разрешено по линиям, параллельным осям координат, поэтому расстояние между двумя точками с координатами x₁, y₁ и x₂, y₂ вычисляется как |x₁ – x₂| + |y₁ – y₂|.

Имеется неизвестная точка A. Вы можете за один запрос узнать расстояние от выбранной точки до точки A. Ваша задача – найти координаты A используя два запроса.

Протокол взаимодействия

Взаимодействие запускается Вашей программой. Вы можете задавать вопросы в формате “? x y” – узнать расстояние от отмеченной точки с координатами x, y до точки A (-10⁶ ≤ x, y ≤ 10⁶, x и y – целые числа).

Если Вы готовы вывести ответ, то используйте следующий формат: “! x y” (x и y – координаты точки A), после чего происходит выход из программы. Это действие не считается запросом.

Примечание

Для корректного взаимодействия выводите конец строки после каждого запроса и после ответа, а также очищайте буфер вывода соответствующими функциями используемого языка программирования:

· cout.flush() или fflush(stdout) для C/C++;

· stdout.flush() для Python;

· смотрите документацию для других языков.

Пример входа	Пример выхода
1 0	? 0 0 ? 1 0 ! 1 0

РЕШЕНИЕ

математика

Анализ алгоритма

Пусть INF = 10⁶. Сделаем два запроса в точках X(-INF, -INF) и Y(INF, -INF).

Пусть O(x, y) – координаты искомой точки.

Пусть d(O, X) = a, d(O, Y) = b. Через d(O, X) обозначено расстояние между точками O и X.

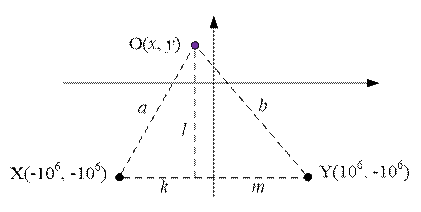
Имеем систему: 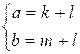, откуда a + b = k + m + 2l. Учитывая что k + m = 2 * INF, имеем: a + b = 2 * INF + 2l. Отсюда l = (a + b – 2 * INF) / 2.

Зная значение l, можно найти y координату искомой точки: y = – INF + l.

Поскольку a = k + l, то k = a – l.

Абсцисса искомой точки равна x = – INF + k = – INF + a – l.

Таким образом искомая точка имеет координаты O(– INF + a – l, – INF + l).

Реализация алгоритма

Определим константу INF = 10⁶.

#define INF 1000000

Функция ask возвращает расстояние res от отмеченной точки до точки (x, y).

int ask(int x, int y)

{

Выводим запрос – узнать расстояние от отмеченной точки до (x, y).

printf("? %d %d\n", x, y);

Очищаем буфер вывода для корректного взаимодействия программы и интерактора.

fflush(stdout);

int res;

Читаем и возвращаем ответ интерактора – расстояние от отмеченной точки до (x, y).

scanf("%d", &res);

return res;

}

Основная часть программы. Узнаем расстояния a = d(O, X) и b = d(O, Y), где O(x, y) – искомая точка, X(-INF, -INF), Y(INF, -INF).

int a = ask(-INF, -INF);

int b = ask(INF, -INF);

Находим длину отрезка l.

int l = (a + b - 2 * INF) / 2;

Вычисляем координаты (x, y) искомой точки.

int x = -INF + a - l;

int y = -INF + l;

Выводим координаты искомой точки и чистим буфер вывода.

printf("! %d %d\n", x, y);

fflush(stdout);

Ниже приводим полную программу.

#include <stdio.h>

#define INF 1000000

int ask(int x, int y)

{

printf("? %d %d\n", x, y);

fflush(stdout);

int res;

scanf("%d", &res);

return res;

}

int main()

{

int a = ask(-INF, -INF);

int b = ask(INF, -INF);

int l = (a + b - 2 * INF) / 2;

int x = -INF + a - l;

int y = -INF + l;

printf("! %d %d\n", x, y);

fflush(stdout);

return 0;

}