11317. K-дисперсия
Рассмотрим дисперсию
последовательности a1, a2, ..., an как
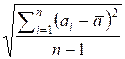
где
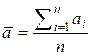
Рассмотрим K-дисперсию как
дисперсию непрерывной подпоследовательности длины k.
Ваша задача – вычислить все (n
– k + 1) K-дисперсии для заданной последовательности и k.
Формально, i-ой (1 ≤
i ≤ n – k + 1) K-дисперсией ri является
дисперсия последовательности {ai, ai+1,
..., ai+k−1}.
Вход. Первая строка содержит два целых
числа n и k (2 ≤ k ≤ n ≤
105).
Вторая строка содержит n целых
чисел a1, a2, ..., an (|ai| ≤ 100).
Выход. Выведите (n – k +
1) строк – действительные числа r1, r2,
..., rn−k+1.
Ответ считается правильным, если
его абсолютная или относительная погрешность не превышает 10-4.
|
Пример
входа 1 |
Пример
выхода 1 |
|
3 2 1 3 2 |
1.41421356 0.70710678 |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
|
5 3 1 3 2 4 5 |
1.00000000 1.00000000 1.52752523 |
РЕШЕНИЕ
математика
Анализ алгоритма
Рассмотрим сумму:
= 
= 
=
– 
+ 
=
– 
+ 
= – 
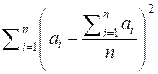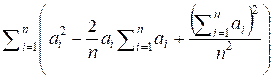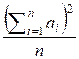Теперь формулу дисперсии можно переписать в виде:
= 
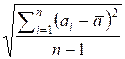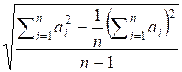
Если для последовательности {ai, ai+1,
..., ai+k−1} поддерживать
сумму ее элементов (ai + ai+1 + ...
+ ai+k−1) и сумму ее квадратов (
),
то за константное время можно вычислить искомую дисперсию на отрезке .
Пример
Распишем числитель дроби в дисперсии для n
= 3:
+ 
+ 
=
= 
–
– 
– 
+
+ 
+ + =
= –
+
=
= –
+
=
= –
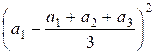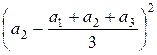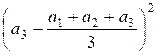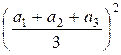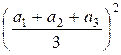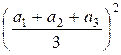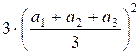Реализация алгоритма
Читаем входные данные.
scanf("%d %d", &n, &k);
a.resize(n);
for (i = 0; i < n; i++)
scanf("%d", &a[i]);
На
отрезке [i – k
+ 1; i] поддерживаем две переменные:
·
сумму sum = ai-k+1 + … + ai-1 + ai,
·
сумму квадратов sum2 = 
sum = sum2 = 0;
Перебираем
элементы последовательности.
for (i = 0; i < n; i++)
{
Обновляем
значения sum и sum2.
sum += a[i];
sum2 += a[i] * a[i];
Если
имеется окно [i – k
+ 1; i] длины k, то выводим ответ для него.
if (i >= k - 1)
{
printf("%lf\n", sqrt((sum2 - (sum * sum) / k) / (k - 1)));
Удаляем
из рассматриваемой последовательности элемент с индексом i – k + 1.
sum -= a[i - k + 1];
sum2 -= a[i - k + 1] * a[i - k +
1];
}
}