11319. Максимизируй это!

По заданным двум целым числам n и m найдите такое действительное число a, что значение f(1/2 + a) является максимальным. Известно, что

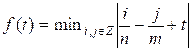
Можно доказать, что максимальное значение функции f(t) рационально. Выведите его в виде несократимой дроби.

Вход. Содержит не более 10⁴ тестов. Каждый тест состоит из одной строки, содержащей два целых числа n и m (1 ≤ n, m ≤ 10⁹).

Выход. Для каждого теста выведите максимальное значение f(1/2 + a) в виде несократимой дроби p / q, где q > 0.

Пример входа	Пример выхода
1 1 1 2	1/2 1/4

РЕШЕНИЕ

математика

Анализ алгоритма

Рассмотрим, какие значения принимает выражение f(i, j) = i / n – j / m, где i, j ∈ Z при фиксированных n и m. Например, f(n, m) = n / n – m / m = 0.

Рассмотрим, например, функцию f(i, j) = i / 3 – j / 5. Тогда

f(i, j) =

Согласно расширенному алгоритму Евклида, всегда существуют такие целые i и j, что i / 3 – j / 5 = 1. Следовательно, наименьшим положительным значением, которое может принимать выражение i / 3 – j / 5, является 1 / 15. Отсюда следует, что это выражение может принимать все возможные значения вида k / 15, где k ∈ Z.

Теорема. Если f(i, j) = i / n – j / m, то эта функция принимает значения вида k / НОК(n, m), где k ∈ Z.

Доказательство. Действительно,

f(i, j) = i / n – j / m = = =

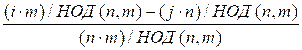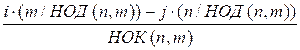
Поскольку числа m / НОД(n, m) и n / НОД(n, m) являются взаимно простыми, то всегда существуют такие i и j, что числитель дроби равен 1. Следовательно, функция f(i, j) может принимать все возможные значения вида k / НОК(n, m), где k ∈ Z.

Теперь рассмотрим исходную функцию

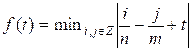
Ее значения – расстояния от точки t до ближайшей точки вида k / НОК(n, m), k ∈ Z. Для максимизации функции f(t) значение t следует выбрать таким образом, чтобы оно находилось точно посередине между соседними точками k / НОК(n, m) и (k + 1) / НОК(n, m), где k – целое число. Значение функции в такой точке равно 1 / 2 * НОК(n, m), что и будет ответом.

Пример

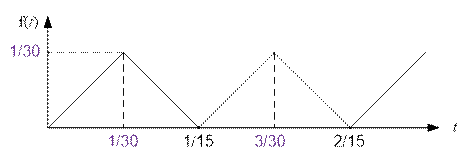
Пусть 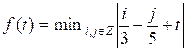. Очевидно, что f(0) = 0. Равенство f(1 / 15) = 0 справедливо, так как существуют такие i и j, что i / 3 – j / 5 = -1 / 15 (например, i = 1, j = 2). Из этого также следует, что f(k / 15) = 0, где k ∈ Z.

Однако f(k / 15 + 1 / 30) = 1 / 30, и это будет наибольшим значением функции, так как точка k / 15 + 1 / 30 находится на максимальном расстоянии от нулей функции.

Реализация алгоритма

Функция gcd вычисляет наибольший общий делитель чисел a и b.

long long gcd(long long a, long long b)

{

return b == 0 ? a : gcd(b, a % b);

}

Функция lcm вычисляет наименьшее общее кратное чисел a и b.

long long lcm(long long a, long long b)

{

return a / gcd(a, b) * b;

}

Основная часть программы. Читаем входные данные.

while (scanf("%lld %lld", &n, &m) == 2)

{

Вычисляем и выводим ответ.

d = 2 * lcm(n, m);

printf("%lld/%lld\n", 1, d);

}