11319. Maximize it!

Given two integers n and m, find a real number a such that the value of f(1/2 + a) is maximized. It is known that

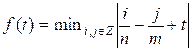
It can be proven that the maximum value of the function f(t) is rational. Print this value in the form of an irreducible fraction.

Input. Contains no more than 10⁴ test cases. Each test case consists of a single line containing two integers n and m (1 ≤ n, m ≤ 10⁹).

Output. For each test case, print the maximum value of f(1/2 + a) in the form of an irreducible fraction p / q, where q > 0.

Sample input	Sample output
1 1 1 2	1/2 ¼

SOLUTION

mathematics

Algorithm analysis

Let’s consider the values that the expression f(i, j) = i / n – j / m takes, where i, j ∈ Z for fixed n and m. For example, f(n, m) = n / n – m / m = 0.

Let’s consider, for instance, the function f(i, j) = i / 3 – j / 5. Then

f(i, j) =

According to the extended Euclidean algorithm, there always exist integers i and j, such that i / 3 – j / 5 = 1. Therefore, the smallest positive value that the expression i / 3 – j / 5 can take is 1 / 15. From this, it follows that this expression can take all possible values of the form k / 15, where k ∈ Z.

Theorem. If f(i, j) = i / n – j / m, then this function takes values of the form k / LCM (n, m), where k ∈ Z.

Proof. Indeed,

f(i, j) = i / n – j / m = = =

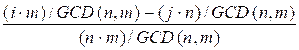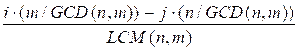
Since the numbers m / GCD (n, m) and n / GCD(n, m) are coprime, there always exists integers i and j such that the numerator of the fraction equals 1. Therefore, the function f(i, j) can take all possible values of the form k / LCM(n, m), where k ∈ Z.

Now let’s consider the original function

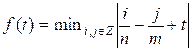
Its values are the distances from the point t to the nearest point of the form k / LCM(n, m), where k ∈ Z. To maximize the function f(t), the value of t should be chosen so that it is exactly in the middle between the neighboring points k / LCM(n, m) and (k + 1) / LCM(n, m), where k is an integer. The value of the function at such a point is 1 / 2 * LCM(n, m), which will be the answer.

Example

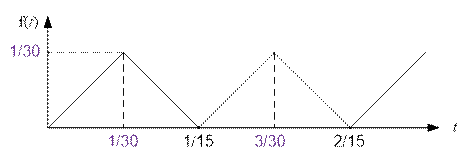
Let 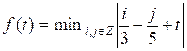. It is obvious that f(0) = 0. The equality f(1 / 15) = 0 holds because there exist integers i and j such that i / 3 – j / 5 = -1 / 15 (for example, i = 1, j = 2). From this, it also follows that f(k / 15) = 0, where k ∈ Z.

However, f(k / 15 + 1 / 30) = 1 / 30, and this will be the maximum value of the function, as the point k / 15 + 1 / 30 is at the maximum distance from the zeros of the function.

Algorithm realization

The gcd function computes the greatest common divisor of the numbers a and b.

long long gcd(long long a, long long b)

{

return b == 0 ? a : gcd(b, a % b);

}

The lcm function computes the least common multiple of the numbers a and b.

long long lcm(long long a, long long b)

{

return a / gcd(a, b) * b;

}

The main part of the program. Read the input data.

while (scanf("%lld %lld", &n, &m) == 2)

{

Compute and print the result.

d = 2 * lcm(n, m);

printf("%lld/%lld\n", 1, d);

}