11320. Amazing trick

Alice is a magician, and she creates a new trick. She has n cards with different numbers from 1 to n written on them. First, she asks an audience member to shuffle the deck and put the cards in a row. Let the number on the i-th card from the left be a_i.

Then Alice selects two permutations p and q. There is a restriction on p and q: permutations can’t have fixed points. In other words, ∀i: p_i ≠ i and q_i ≠ i.

Once the permutations are chosen, Alice shuffles the cards according to them. Now the i-th card from the left becomes the card a[p[q[i]]. The trick is considered successful if, after shuffling, the number on the i-th card from the left is i.

Help Alice choose the permutations p and q, or determine if it is impossible for the given starting permutation a.

Input. The first line contains the number of test cases t (1 ≤ t ≤ 10⁵).

Each test is described in two lines. The first line contains one integer n (1 ≤ n ≤ 10⁵) – the number of cards. The second line contains n integers a_i (1 ≤ a_i ≤ n, ∀i ≠ j: a_i ≠ a_j) – the initial permutation of the cards.

It is guaranteed that the sum of n over all tests does not exceed 10⁵.

Output. Print the answer for each test case in the order they appear in the input.

For each test case, print “Impossible” on a single line if no solution exists.

Otherwise, print “Possible” on the first line, followed by two lines containing the permutations p and q.

Sample input	Sample output
4 2 2 1 3 1 2 3 4 2 1 4 3 5 5 1 4 2 3	Impossible Possible 3 1 2 2 3 1 Possible 3 4 2 1 3 4 2 1 Possible 4 1 2 5 3 3 1 4 5 2

SOLUTION

combinatorics

Algorithm analysis

Let’s consider three permutations: a, p, and q. Let I be the identity permutation. Consider the equation: a(p(q( I ))) = I. From this, we get p(q( I )) = a^-1. Using the fact that permutations are applied from right to left, this identity can be rewritten as: p _° q = a^-1. Therefore, q = p^-1 _° a^-1.

Generate a random permutation p that has no fixed points. Then, compute the permutation q = p^-1 _° a^-1 and check that it has no fixed points. The found permutations p and q are the required ones.

Example

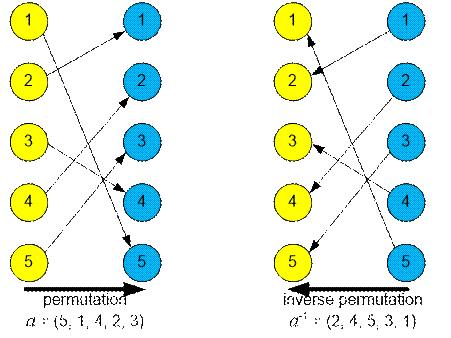
Consider the permutation a = (5, 1, 4, 2, 3).

Its inverse will be a^-1 = (2, 4, 5, 3, 1).

Generate a random permutation p with no fixed points. For example, let p = (4, 1, 2, 5, 3). Now, let’s compute its inverse: p^-1 = (2, 3, 5, 1, 4).

Next, compute q = p^-1 _° a^-1 = (2, 3, 5, 1, 4) _° (2, 4, 5, 3, 1) = (3, 1, 4, 5, 2). The permutation q has no fixed points, so it is valid.

Algorithm realization

The print function prints the elements of the array a, starting from the first one.

void print(vector<int>& a)

{

for (int i = 1; i < a.size(); i++)

printf("%d ", a[i]);

printf("\n");

}

The function is_valid checks whether the permutation v contains any fixed points.

bool is_valid(vector<int>& v)

{

for (int i = 1; i < v.size(); i++)

if (v[i] == i) return false;

return true;

}

Declare the arrays.

vector<int> a, p, p1, q;

The main part of the program. Read the input data.

scanf("%d", &tests);

while (tests--)

{

scanf("%d", &n);

Initialize the arrays.

a.resize(n + 1);

p1.resize(n + 1);

p.resize(n + 1);

q.resize(n + 1);

Read the input permutation a and immediately store its inverse in the array a. That is, the array a contains the permutation a^-1, where a is the input permutation.

for (i = 1; i <= n; i++)

{

scanf("%d", &x);

a[x] = i;

}

mt19937 is one of the standard pseudorandom number generators in C++ (Mersenne Twister with a period of 19937). It is very fast and has good statistical properties, making it an excellent choice for most tasks requiring random number generation.

mt19937 gen(random_device{}());

In the variable found, we’ll mark whether a solution is found for the current test.

found = false;

Perform 1000 iterations.

for (it = 0; it < 1000; it++)

{

Generate a random permutation. To do this, populate the array p with the numbers 0, 1, 2, …, and use the shuffle function to shuffle the elements, starting from the first (non-zero) element. We work with permutations from 1 to n.

iota(p.begin(), p.end(), 0);

shuffle(p.begin() + 1, p.end(), gen);

Check whether the permutation p is valid (i.e., it contains no fixed points).

if (!is_valid(p)) continue;

Compute the permutation p1 = p^-1.

for (i = 1; i <= n; i++)

p1[p[i]] = i;

Compute the permutation q = p1 _° a^-1 = p^-1 _° a^-1.

for (i = 1; i <= n; i++)

q[i] = p1[a[i]];

If the permutation q is valid, print the result.

if (is_valid(q))

{

puts("Possible");

print(p);

print(q);

found = true;

break;

}

}

If no solution is found after 1000 iterations, then no solution exists.

if (!found) puts("Impossible");

}