11340. Радио 106
FM
Вам дан список песен, которые
играли на радио 106 FM. Всего в списке содержится n песен. Найдите длину
самого длинного фрагмента списка, состоящего из неповторяющихся песен.
Вход. Первая строка содержит количество
песен n (1 ≤ n ≤ 105) в списке.
Вторая строка содержит n целых чисел k1, k2,
..., kn (1 ≤ ki
≤ 109) – идентификационные номера песен.
Выход. Выведите длину самого длинного
фрагмента списка, состоящего из неповторяющихся песен.
|
Пример
входа 1 |
Пример
выхода 1 |
|
8 1 2 1 3 2 7 4 2 |
5 |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
|
4 1 1 2 1 |
2 |
РЕШЕНИЕ
структуры
данных - set
Анализ алгоритма
Пусть массив v хранит идентификационные номера песен. С помощью двух указателей будем поддерживать скользящее
окно [i;
j], в котором песни не повторяются. Иными словами, на
отрезке [i;
j] все песни уникальны.
Песни из этого отрезка будем хранить во множестве s. Для каждого значения i
будем стремиться расширить отрезок до максимальной возможной длины. То есть для фиксированного i будем искать такое j,
что на отрезке [i;
j] песни не
повторяются, а на отрезке [i; j + 1] уже появляются дубли.
При обработке текущей песни с
индексом j + 1 имеются два варианта:
·
если песня vj+1 не встречается в отрезке [i; j], то добавляем ее в этот
отрезок, расширяя его до [i; j + 1];
·
если песня vj+1 уже присутствует в отрезке, сдвигаем левую границу i вправо до тех пор, пока vj+1 не исчезнет из отрезка [i; j]. Затем добавляем vj+1 в отрезок, расширяя его до [i; j + 1]. При каждом сдвиге i удаляем соответствующие
элементы из множества s;
Среди всех возможных
отрезков [i;
j] с уникальными
песнями находим максимальную длину. Это и будет
ответом на задачу.
Пример
Рассмотрим как
будут изменяться отрезки с неповторяющимися песнями для первого примера.
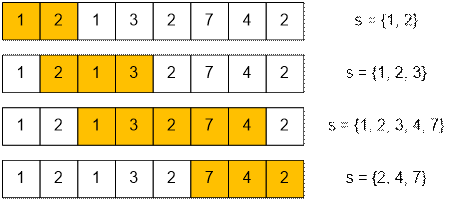
Длина
наибольшего отрезка равна 5.
Реализация алгоритма
Читаем входные данные. Идентификационные номера песен храним в массиве v.
scanf("%d", &n);
v.resize(n);
for (i = 0; i < n; i++)
scanf("%d", &v[i]);
Поддерживаем отрезок [i; j – 1] из неповторяющихся песен (то есть песни от vi до vj-1 не повторяются). Во
множестве s храним идентификационные номера
песен из этого отрезка. В переменной res отслеживаем длину самого длинного фрагмента с уникальными песнями.
i = res =
0;
for (j = 0; j < n; j++)
{
Рассматриваем текущую песню с индексом j. Если она уже содержится во множестве s, то расширить текущий отрезок [i; j – 1] за счет j-ой песни не удастся.
В этом случае необходимо сдвигать левую границу i, удаляя из множества s песню vi, до тех пор, пока j-ая
песня не исчезнет из множества s.
while (s.find(v[j]) != s.end())
{
s.erase(v[i]);
i++;
}
Добавим j-ую песню в отрезок и,
соответственно, во множество s. Таким образом,
отрезок [i;
j] не будет содержать повторяющихся песен.
s.insert(v[j]);
Среди всех возможных отрезков [i; j] находим самый длинный.
Длина отрезка [i; j] равна j – i + 1.
res = max(res, j - i + 1);
}
Выводим ответ.
printf("%d\n", res);