11340. Radio 106 FM
You are given a list of songs that are
played on Radio 106 FM. The list contains a total of n songs. Find
the length of the longest fragment of the list that consists of non-repeating
songs.
Input. The first line contains the number of songs n (1 ≤ n ≤ 105) in the list. The second line
contains n integers k1, k2, ..., kn (1
≤ ki ≤ 109), which are the identification numbers of
the songs.
Output. Print the length of the longest fragment of the list
that consists of unique songs.
|
Sample
input 1 |
Sample
output 1 |
|
8 1 2 1 3 2 7 4 2 |
5 |
|
|
|
|
Sample
input 2 |
Sample
output 2 |
|
4 1 1 2 1 |
2 |
SOLUTION
data structures - set
Algorithm analysis
Let the array v
store the identification numbers of the songs. Using two pointers, we will
maintain a sliding window [i; j] in which the songs do not
repeat. In other words, all the songs in the segment [i; j] are unique. The songs
from this segment will be stored in a set s. For each value of i,
we will try to extend the segment to the maximum possible length. That is, for
a fixed i, we will search for such a j that in the segment [i; j] the songs do not repeat,
but in the segment [i; j + 1] duplicates already appear.
When processing the current song at index j + 1, there are two possible cases:
·
If the
song vj+1 is not present in the segment [i;
j], add it to this segment, extending it to [i; j + 1];
·
If the
song vj+1 is already present in the segment, shift the left
boundary i to the right until vj+1 disappears
from the segment [i; j]. Then, add vj+1 to the segment, extending it to [i; j + 1]. With each shift of i, remove the
corresponding elements from the set s;
Among all possible
segments [i;
j] with
unique songs, find the maximum length. This will be the answer to the problem.
Example
Let’s consider how the
segments with unique songs will change for the first example.
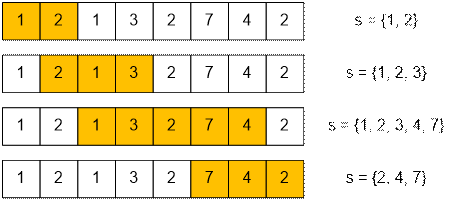
The length of the longest segment
is 5.
Algorithm realization
Read
the input data. The identification numbers of the songs are stored in the array v.
scanf("%d", &n);
v.resize(n);
for (i = 0; i < n; i++)
scanf("%d", &v[i]);
Maintain
the segment [i; j – 1] of unique songs (i.e., the songs from vi to vj-1 do not repeat). In the set s, store
the identification numbers of the songs from this segment. The variable res
tracks the length of the longest fragment with unique songs.
i = res =
0;
for (j = 0; j < n; j++)
{
Consider
the current song at index j. If it is already in the set s, it
will not be possible to extend the current segment [i; j – 1] by
including the j-th song. In this case, we need to shift the left
boundary i, removing the song vi from the set s, until the j-th song disappears from the
set s.
while (s.find(v[j]) != s.end())
{
s.erase(v[i]);
i++;
}
Add
the j-th song to the segment and, accordingly, to the set s.
Thus, the segment [i; j] will not contain any repeated songs.
s.insert(v[j]);
Among
all possible segments [i; j], find the longest one. The length of the
segment [i;
j] is j – i + 1.
res = max(res, j - i + 1);
}
Print
the answer.
printf("%d\n", res);