11343. Шеф и двудольный граф

Шеф заинтересовался изучением двудольных графов. Сегодня он хочет построить двудольный граф с n вершинами в каждой из двух частей и с общим числом ребер, равным m. Вершины слева пронумерованы от 1 до n. Вершины справа тоже пронумерованы от 1 до n. Он также хочет, чтобы степень каждой вершины была больше или равна d и меньше или равна D, то есть для всех v: d ≤ deg(v) ≤ D.

По четырем целым числам n, m, d, D Вы должны помочь Шефу построить некоторый двудольный граф, удовлетворяющий описанному свойству. Если такого графа не существует, выведите -1.

Вход. Первая строка содержит количество тестов t.

Одна строка каждого набора входных данных содержит четыре целых числа n (1 ≤ n ≤ 100), m (0 ≤ m ≤ n * n), d, D (1 ≤ d ≤ D ≤ n).

Выход. Для каждого набора входных данных выведите -1, если не существует двудольного графа, удовлетворяющего заданному свойству. В противном случае выведите m строк, каждая из которых должна содержать два целых числа u и v, обозначающие наличие ребра между вершиной u в левой части и вершиной v в правой части. Если существует несколько возможных ответов, выведите любой. Обратите внимание, что двудольный граф не должен иметь кратных ребер.

Пример входа	Пример выхода
2 2 3 1 2 2 3 1 1	1 1 2 2 1 2 -1

РЕШЕНИЕ

поиск в глубину

Анализ алгоритма

В левой и правой долях графа располагается n вершин. Поскольку степень каждой вершины больше или равна d и меньше или равна D, то число ребер m должно быть как минимум n * d (n * d ≤ m) и максимум n * D (n * D ≥ m).

Граф будем строить конструктивно следующим образом.

1. Пусть cur = 0.

2. Для каждого i (1 ≤ i ≤ n) соединим вершину i левой доли с вершиной i + cur правой доли. Если окажется i + cur > n, то в правой доле используем вершину i + cur – n. Как только будет построено m ребер, завершаем алгоритм.

3. cur = cur + 1 и переходим к пункту 2.

Пример

Граф из примера имеет следующий вид:

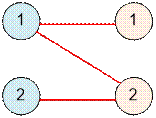
Реализация алгоритма

Читаем количество тестов tests.

scanf("%d", &tests);

while (tests--)

{

Читаем входные данные очередного теста.

scanf("%d %d %d %d", &n, &m, &d, &D);

Если граф построить нельзя из-за невыполнения необходимых неравенств, то выводим -1.

if (n * d > m || n * D < m)

{

printf("-1\n");

continue;

}

Установим cur = 0.

cur = 0;

while (m > 0)

{

Пока не будет построено в точности m ребер, строим ребра по указанному алгоритму.

for (i = 1; i <= n; i++)

{

j = (i + cur) % n;

if (j == 0) j = n;

Выводим ребро (i, j).

printf("%d %d\n", i, j);

m--;

Как только будут построены все m ребер, завершаем программу.

if (m == 0) break;

}

Увеличим значение переменной cur на 1.

cur++;

}

}