11389. Игра Хусейна

У Хусейна есть строка, состоящая из символов 0 и 1. Чтобы развлечься, он придумал следующую игру. Хусейн может выполнять одну из двух операций над строкой:

· приписать с левого конца 0, а с правого 1;

· приписать с правого конца 0, а с левого 1;

Например, из строки 010 можно получить 00101 или 10100.

Вам дана строка, полученная после выполнения всех операций (возможно, Хусейн не сделал ни одной операции). Определите, какой могла быть наименьшая возможная длина строки до начала изменений.

Вход. Одна строка длины не более 10⁵, содержащая только символы 0 и 1.

Выход. Выведите наименьшую возможную длину строки, которая изначально могла быть у Хусейна.

Пример входа 1	Пример выхода 1
01010010	8
Пример входа 2	Пример выхода 2
1001110	1

РЕШЕНИЕ

два указателя

Анализ алгоритма

Рассмотрим входную строку s – результирующую строку Хусейна после выполнения всех операций. Инициализируем два указателя: i = 0 на начало и j = n – 1 на конец строки. 

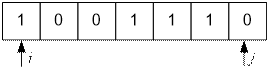
Если s_i ≠ s_j, то на концах строки находятся разные символы. А именно или 0 слева и 1 справа, или 1 слева и 0 справа. Это значит, что предыдущая строка могла быть увеличена в результате применения одной из заданных операций. В этом случае сдвигаем оба указателя i и j на одну позицию навстречу друг другу и снова проверяем, могла ли подстрока s[i ... j] быть получена в результате операций Хусейна.

Как только для текущей подстроки s[i ... j] будет выполняться s_i = s_j, ее уже нельзя получить при помощи данных операций. Выводим ее длину – это и будет исходная строка Хусейна.

Пример

Проведем операции Хусейна в обратном порядке.

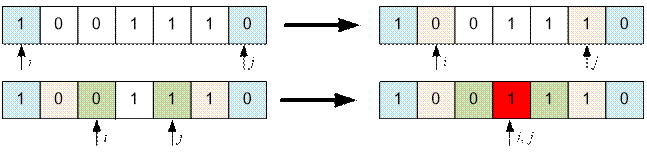
Строка s = “1” изначально была у Хусейна.

Реализация алгоритма

Читаем входную строку. Вычисляем ее длину в переменной res.

cin >> s;

res = s.size();

Инициализируем два указателя: i = 0 на начало и j = n – 1 на конец строки. 

i = 0; j = s.size() - 1;

Если s_i ≠ s_j, то на концах строки находятся разные символы. Хусейн мог при помощи своей операции получить строку s[i ... j] из строки s[i + 1 ... j – 1].

while ((i < j) && (s[i] != s[j]))

{

Сдвигаем оба указателя i и j на одну позицию навстречу друг другу и уменьшаем на 2 текущий размер res подстроки s[i ... j].

i++; j--;

res -= 2;

}

Выводим ответ.

cout << res << endl;