11428. Tree diameter
A tree consisting of n vertices
is given.
The diameter of a tree is
the maximum distance between two vertices. Find the diameter of the given tree.
Input. The first line contains an integer n (1 ≤ n ≤ 2 * 105) – the number of vertices in the tree. The
vertices are numbered from 1 to n.
Each of the following n – 1 lines
describes an edge and contains two integers a and b (1 ≤ a, b ≤
n), indicating that
there is an edge between vertices a and b.
Output. Print one integer – the diameter of the tree.
|
Sample
input |
Sample
output |
|
5 1 2 1 3 3 4 3 5 |
3 |
SOLUTION
graphs – depth first search
Algorithm analysis
Perform a depth-first
search starting from any vertex, for example, from vertex 1. Find the vertex
farthest from 1 and denote it as vertex a. Then, start a depth-first
search from vertex a to find the vertex that is farthest from a,
which we’ll denote as vertex b. The distance between vertices a
and b will then be the maximum possible and equal to the diameter of the
tree.
Example
Consider the tree from the example.
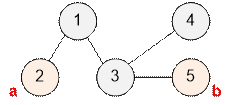
The diameter of the tree is 3.
The maximum distance is achieved, for example, between vertices 2 and 5.
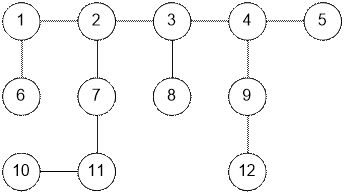
Exercise
Find the diameter of the
tree.
Algorithm implementation
Store
the input tree in the adjacency list g. Store the shortest distances from the
source to each vertex in the array dist.
vector<vector<int>> g;
vector<int> dist;
The dfs function performs
a depth-first search from vertex v. The shortest distance from the
source to vertex v is d. The parent of
vertex v in the depth-first search is p.
void dfs(int v, int d, int p = -1)
{
Store
the shortest distance from the source to vertex v in dist[v].
dist[v] = d;
Iterate
over all edges (v, to). For each
son to of vertex v (where to is
not a parent of v) initiate a depth-first search. The distance from the
source to vertex to will be d + 1.
for (int to : g[v])
if (to != p) dfs(to, d + 1, v);
}
The
main part of the program. Read the input data.
scanf("%d", &n);
g.resize(n
+ 1);
dist.resize(n
+ 1);
Construct
an undirected tree.
for (i = 1; i < n; i++)
{
scanf("%d %d", &u, &v);
g[u].push_back(v);
g[v].push_back(u);
}
Find
the shortest distances from vertex 1 to all other vertices. The vertex farthest
from it is a.
dfs(1, 0,
-1);
a =
max_element(dist.begin(), dist.begin() + n + 1) –
dist.begin();
Find
the shortest distances from vertex b to all other vertices. The vertex
farthest from it is b.
dfs(a,
0, -1);
b =
max_element(dist.begin(), dist.begin() + n + 1) –
dist.begin();
Print
the diameter of the tree – the shortest distance from a to b.
printf("%d\n", dist[b]);