11429. Подчиненные

По заданной структуре компании вычислите количество подчиненных для каждого сотрудника.

Вход. В первой строке находится целое число n (1 ≤ n ≤ 2 * 10⁵) – количество сотрудников. Сотрудники пронумерованы числами 1, 2, ..., n. Сотрудник номер 1 является генеральным директором компании.

Далее следуют n – 1 целых чисел: для каждого сотрудника 2, 3, ... , n указан их непосредственный начальник в компании.

Выход. Выведите n целых чисел. Для каждого сотрудника 1, 2, ..., n выведите количество его подчиненных.

Пример входа	Пример выхода
5 1 1 2 3	4 1 1 0 0

РЕШЕНИЕ

графы – поиск в глубину

Анализ алгоритма

Структурой компании является дерево. Для каждой вершины дерева v необходимо определить количество вершин sum[v] в поддереве, где она является корнем. Тогда количество подчиненных у сотрудника v будет равно sum[v] – 1 (поскольку сотрудник v не является собственным подчиненным).

Запустим поиск в глубину из вершины 1, которая соответствует генеральному директору компании. Если to₁, to₂, …, to_k – сыновья вершины v, то

sum[v] = 1 + sum[to₁] + sum[to₂] + … + sum[to_k]

Если вершина v является листом дерева, то установим sum[v] = 1.

Пример

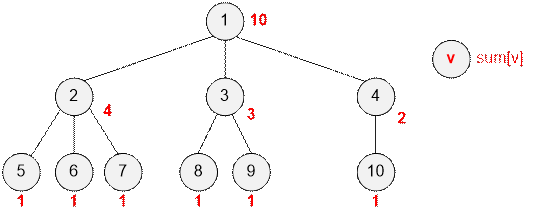
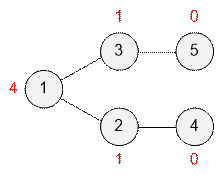
Рассмотрим пример. Возле каждого сотрудника (вершины графа) указано количество его подчиненных.

Реализация алгоритма

Дерево храним в списке смежности g.

vector<vector<int> > g;

Функция dfs выполняет поиск в глубину из вершины v и возвращает количество вершин в поддереве с корнем v. Вершина p является предком v при поиске в глубину.

int dfs(int v, int p)

{

Поддерево с корнем v изначально содержит только одну вершину – вершину v.

sum[v] = 1;

Рассматриваем ребро v → to. Если to ≠ p, то добавляем к sum[v] количество вершин в поддереве с корнем to.

for (int to : g[v])

if (to != p) sum[v] += dfs(to, v);

Возвращаем количество вершин в поддереве с корнем v.

return sum[v];

}

Основная часть программы. Читаем входные данные. Строим дерево.

scanf("%d", &n);

g.resize(n + 1);

for (i = 2; i <= n; i++)

{

scanf("%d", &x);

Для сотрудника i непосредственным начальником в компании является x.

g[i].push_back(x);

g[x].push_back(i);

}

Запускаем поиск в глубину из вершины 1.

sum.resize(n + 1);

dfs(1, -1);

Выводим ответ. Количество подчиненных сотрудника i равно sum[i] – 1.

for (i = 1; i <= n; i++)

printf("%d ", sum[i] - 1);

printf("\n");

Java реализация

import java.util.*;

public class Main

{

static ArrayList<Integer>[] g;

static int sum[];

static int n;

static int dfs(int v, int p)

{

sum[v] = 1;

for(int to : g[v])

if (to != p) sum[v] += dfs(to,v);

return sum[v];

}

@SuppressWarnings("unchecked")

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

n = con.nextInt();

g = new ArrayList[n+1]; // unchecked

sum = new int[n+1];

for (int i = 0; i <= n; i++)

g[i] = new ArrayList<Integer>();

for (int i = 2; i <= n; i++)

{

int x = con.nextInt();

g[i].add(x);

g[x].add(i);

}

dfs(1,-1);

for (int i = 1; i <= n; i++)

System.out.print(sum[i] - 1 + " ");

System.out.println();

con.close();

}

}

Python реализация

Увеличим стек для рекурсии.

import sys

sys.setrecursionlimit(1000000)

Функция dfs выполняет поиск в глубину из вершины v и возвращает количество вершин в поддереве с корнем v. Вершина p является предком v при поиске в глубину.

def dfs(v, p):

Поддерево с корнем v изначально содержит только одну вершину – вершину v.

sum[v] = 1

Рассматриваем ребро v → to. Если to ≠ p, то добавляем к sum[v] количество вершин в поддереве с корнем to.

for to in g[v]:

if to != p: sum[v] += dfs(to,v)

Возвращаем количество вершин в поддереве с корнем v.

return sum[v]

Основная часть программы. Читаем количество сотрудников n.

n = int(input())

Инициализируем список смежности графа g.

g = [[] for _ in range(n+1)]

Читаем входные данные. Строим дерево.

lst = list(map(int, input().split()))

for i in range(2,n+1):

a = lst[i-2]

Для сотрудника i (i ≥ 2) непосредственным начальником в компании является a.

g[a].append(i)

g[i].append(a)

Инициализируем список sum.

sum = [0] * (n + 1)

Запускаем поиск в глубину из вершины 1.

dfs(1,-1)

Выводим ответ. Количество подчиненных сотрудника i равно sum[i] – 1.

for i in range(1, n+1):

print(sum[i] - 1,end=" ")