11429. Subordinates
Given the company’s structure, your task is
to determine the number of subordinates for each employee.
Input. The first line contains an integer n (1 ≤ n ≤ 2 * 105)
– the number of employees. Employees
are numbered 1, 2, ...,
n, with employee 1 being
the general director of the company.
Then n – 1 integers follow: for each
employee 2, 3, ..., n their direct boss in the company.
Output. Print n integers: for each employee 1, 2, ..., n the number of their subordinates.
|
Sample
input |
Sample
output |
|
5 1 1 2 3 |
4 1 1 0 0 |
SOLUTION
graphs – depth first search
Algorithm analysis
The
structure of the company is a tree. For each vertex v in the tree, determine
the number of vertices sum[v] in the subtree where v is the root.
The number of subordinates for employee v will be sum[v] – 1 (since
employee v is not his own subordinate).
Initiate a
depth-first search starting from vertex 1, which corresponds to the general
director of the company. If to1, to2, …, tok
are the children of vertex v, then
sum[v] = 1 + sum[to1]
+ sum[to2] + … + sum[tok]
If vertex v is a leaf in the tree,
set sum[v] = 1.
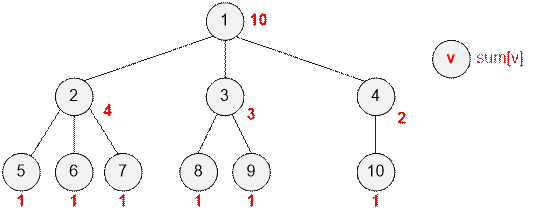
Example
Consider the example. Next to each
employee (vertex of the graph), the number of their subordinates is indicated.
Algorithm implementation
The
tree is stored in the adjacency list g.
vector<vector<int> > g;
The
dfs function performs a depth-first search from vertex v
and returns the number of vertices in the subtree rooted at v. Vertex p
is the parent of v in the depth-first search.
int dfs(int v, int p)
{
Initially,
the subtree rooted at v contains only the vertex v.
sum[v] = 1;
Consider
the edge v → to. If to ≠ p, add to sum[v]
the number of vertices in the subtree rooted at to.
for (int to : g[v])
if (to != p)
sum[v] +=
dfs(to, v);
Return
the number of vertices in the subtree rooted at v.
return sum[v];
}
The
main part of the program. Read the input data. Construct a tree.
scanf("%d", &n);
g.resize(n
+ 1);
for (i = 2; i <= n; i++)
{
scanf("%d", &x);
For
employee i, its immediate supervisor in the company is x.
g[i].push_back(x);
g[x].push_back(i);
}
Start
the depth-first search from vertex 1.
sum.resize(n
+ 1);
dfs(1, -1);
Print
the answer. The number of subordinates of employee i is equal to sum[i]
– 1.
for (i = 1; i <= n; i++)
printf("%d ", sum[i] - 1);
printf("\n");
Java implementation
import java.util.*;
public class Main
{
static
ArrayList<Integer>[] g;
static int sum[];
static int n;
static int dfs(int v, int p)
{
sum[v] = 1;
for(int to : g[v])
if (to != p) sum[v] += dfs(to,v);
return sum[v];
}
@SuppressWarnings("unchecked")
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
n = con.nextInt();
g = new ArrayList[n+1]; // unchecked
sum = new int[n+1];
for (int i = 0; i <= n; i++)
g[i] = new ArrayList<Integer>();
for (int i = 2; i <= n; i++)
{
int x = con.nextInt();
g[i].add(x);
g[x].add(i);
}
dfs(1,-1);
for (int i = 1; i <= n; i++)
System.out.print(sum[i] - 1 + " ");
System.out.println();
con.close();
}
}
Python implementation
Increase
the stack for recursion.
import sys
sys.setrecursionlimit(1000000)
The
dfs function performs a depth-first search from vertex v
and returns the number of vertices in the subtree rooted at v. Vertex p
is the parent of v in the depth-first search.
def dfs(v, p):
Initially,
the subtree rooted at v contains only the vertex v.
sum[v] = 1
Consider
the edge v → to. If to ≠ p, add to sum[v]
the number of vertices in the subtree rooted at to.
for to in g[v]:
if to != p: sum[v] += dfs(to,v)
Return
the number of vertices in the subtree rooted at v.
return sum[v]
The
main part of the program. Read the number of employees.
n = int(input())
Initialize
the adjacency list of the graph g.
g = [[] for _ in
range(n+1)]
Read
the input data. Construct a tree.
lst = list(map(int, input().split()))
for i in range(2,n+1):
a = lst[i-2]
For
employee i (i ≥ 2), its immediate supervisor in the company
is a.
g[a].append(i)
g[i].append(a)
Initialize
the list sum.
sum = [0] * (n + 1)
Start
the depth-first search from vertex 1.
dfs(1,-1)
Print
the answer. The number of subordinates of employee i is equal to sum[i]
– 1.
for i in range(1, n+1):
print(sum[i] - 1,end=" ")