11430. Расстояние
на дереве I
Задано дерево, состоящее из n вершин.
Для каждой вершины определите
наибольшее расстояние до другой вершины.
Вход. Первая строка содержит целое число n (1 ≤ n ≤ 2 * 105) – количество вершин. Вершины
пронумерованы 1, 2, ..., n.
Следующие n – 1 строк
описывают ребра. Каждая строка содержит два целых числа a и b (1 ≤ a, b ≤ n), означающие что между вершинами a и b имеется ребро.
Выход. Выведите n целых чисел: для каждой вершины 1, 2, ..., n максимальное расстояние до другой вершины.
|
Пример
входа |
Пример
выхода |
|
5 1 2 1 3 3 4 3 5 |
2 3 2 3 3 |
РЕШЕНИЕ
графы –
поиск в глубину
Анализ алгоритма
При помощи двух поисков в глубину найдем диаметр дерева. Поскольку
дерево является связным графом, в котором отсутствуют циклы, то и поиск в
глубину, и поиск в ширину найдет кратчайшие расстояния от источника (стартовой
вершины).
Пусть a и b – две вершины,
находящиеся на максимальном расстоянии друг от друга. Вычислим кратчайшие расстояния от a и b до остальных
вершин в массивах dista и distb. Тогда наибольшее расстояние от вершины i до другой равно
max(dista[i], distb[i])
Пример
Рассмотрим дерево
из примера.
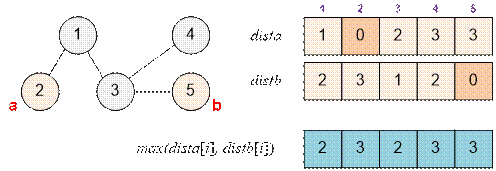
Диаметром дерева
будет, например, расстояние между вершинами 2 и 5.
Реализация алгоритма
Входное дерево храним в списке смежности g. Кратчайшие расстояния от вершин a и b храним в массивах dista и distb.
vector<vector<int>> g;
vector<int> dista, distb;
Читаем количество вершин n в дереве.
scanf("%d", &n);
Функция dfs совершает поиск в глубину из вершины v. Кратчайшее расстояние от источника до вершины
v равно d. Кратчайшие расстояния от источника до вершин
сохраняются в массиве dist. Предком вершины v при поиске в глубину является p.
void dfs(int v, int d, vector<int>&
dist, int p = -1)
{
Заносим в dist[v]
кратчайшее
расстояние от источника до вершины v.
dist[v] = d;
Перебираем ребра (v, to). Для каждого сына to вершины v (вершина to не является предком вершины v) запускаем поиск в
глубину.
for (int to : g[v])
if (to != p)
dfs(to, d + 1, dist, v);
}
Основная часть программы. Читаем входные данные.
scanf("%d", &n);
g.resize(n
+ 1);
dista.resize(n
+ 1);
distb.resize(n
+ 1);
Строим неориентированное дерево.
for (i = 1; i < n; i++)
{
scanf("%d %d", &u, &v);
g[u].push_back(v);
g[v].push_back(u);
}
Ищем кратчайшие расстояния от вершины 1. Самой дальней вершиной от 1
является вершина a.
dfs(1,
0, dista, -1);
a =
max_element(dista.begin() + 1,
dista.begin() + n + 1) - dista.begin();
Ищем кратчайшие расстояния от вершины a, сохраняем их в массиве dista. Самой дальней
вершиной от a является вершина b. Расстояние от a до b есть диаметр графа.
dfs(a,
0, dista, -1);
b =
max_element(dista.begin() + 1,
dista.begin() + n + 1) - dista.begin();
Ищем кратчайшие расстояния от вершины b, сохраняем их в массиве distb.
dfs(b,
0, distb, -1);
Для каждой вершины i
выводим
самую дальнюю вершину.
for (i = 1; i <= n; i++)
printf("%d ", max(dista[i], distb[i]));
printf("\n");
Python реализация
import sys
sys.setrecursionlimit(1000000)
Функция dfs совершает поиск в глубину из вершины v. Кратчайшее расстояние от источника до вершины
v равно d. Кратчайшие расстояния от источника до вершин
сохраняются в списке dist. Предком вершины v при поиске в глубину является p.
def dfs(v, d, dist, p =- 1):
Заносим в dist[v]
кратчайшее
расстояние от источника до вершины v.
dist[v] = d
Перебираем ребра (v, to). Для каждого сына to вершины v (вершина to не является предком вершины v) запускаем поиск в
глубину.
for to in g[v]:
if to != p:
dfs(to, d + 1, dist, v)
Основная часть программы. Читаем входные данные.
n = int(input())
g = [[] for _ in range(n + 1)]
dista = [0] * (n + 1)
distb = [0] * (n + 1)
Строим неориентированное дерево.
for _ in range(n - 1):
u,
v = map(int, input().split())
g[u].append(v)
g[v].append(u)
Ищем кратчайшие расстояния от вершины 1. Самой дальней вершиной от 1
является вершина a.
dfs(1, 0, dista)
a = dista.index(max(dista[1:]))
Ищем кратчайшие расстояния от вершины a, сохраняем их в массиве dista. Самой дальней
вершиной от a является вершина b. Расстояние от a до b есть диаметр графа.
dfs(a, 0, dista)
b = dista.index(max(dista[1:]))
Ищем кратчайшие расстояния от вершины b, сохраняем их в массиве distb.
dfs(b, 0, distb)
Для каждой вершины i
выводим
самую дальнюю вершину.
result = [max(dista[i], distb[i]) for i in range(1, n + 1)]
print(*result)