11430. Tree distances I
A tree consisting of n vertices is
given.
For each vertex, determine the maximum
distance to any other vertex.
Input. The first line contains an integer n (1 ≤ n ≤ 2 * 105) – the
number of vertices in the tree. The vertices are numbered from 1 to n.
The next n – 1 lines
describe the edges: each line contains two integers a and b (1 ≤ a, b ≤ n), indicating that there is an edge between vertices a
and b.
Output. Print n integers.
For each vertex from 1 to n, print the maximum distance to any other
vertex in the tree.
|
Sample
input |
Sample
output |
|
5 1 2 1 3 3 4 3 5 |
2 3 2 3 3 |
РЕШЕНИЕ
graphs – depth first search
Algorithm analysis
Using two depth-first search (DFS) runs, we find the diameter of the tree.
Since a tree is a connected graph without cycles, both depth-first search
(DFS) and breadth-first search (BFS) correctly find the shortest distances from
the starting vertex to all others.
Let a and b be two vertices that are the farthest apart – that
is, they define the diameter of the tree.
Compute the shortest distances from vertex a to all other vertices
and store them in the array dista, and from vertex b – in the
array distb.
Then, for each vertex i, the greatest distance to any other vertex
is equal to:
max(dista[i], distb[i])
Example
Consider a tree from the example.
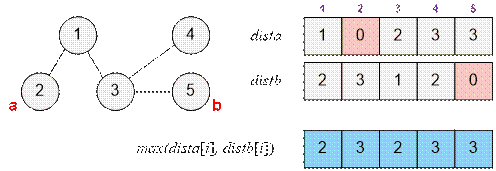
The diameter of the tree
can be, for example, the path between vertices 2 and 5.
Algorithm implementation
The
input tree is stored as an adjacency list g.
The
shortest distances from vertices a and b are stored in the arrays
dista and distb, respectively.
vector<vector<int>> g;
vector<int> dista, distb;
The function dfs performs
a depth-first search starting from vertex v.
·
The parameter d represents the shortest distance from the
source to vertex v.
·
The results are stored in the array dist.
·
The parameter p indicates the parent of vertex v
during the traversal.
void dfs(int v, int d, vector<int>&
dist, int p = -1)
{
Store
the shortest distance from the source to vertex v in dist[v].
dist[v] = d;
Iterate
over all edges (v, to). For each child to
of vertex v (i.e., a vertex to that is not the parent of v),
perform a depth-first search.
for (int to : g[v])
if (to != p)
dfs(to, d + 1, dist, v);
}
The
main part of the program. Read the input data.
scanf("%d", &n);
g.resize(n
+ 1);
dista.resize(n
+ 1);
distb.resize(n
+ 1);
Construct
an undirected tree.
for (i = 1; i < n; i++)
{
scanf("%d %d", &u, &v);
g[u].push_back(v);
g[v].push_back(u);
}
Compute
the shortest distances from vertex 1. The vertex farthest from it is vertex a.
dfs(1,
0, dista, -1);
a =
max_element(dista.begin() + 1,
dista.begin() + n + 1) - dista.begin();
Next,
compute the shortest distances from vertex a and store them in the array
dista. The vertex farthest from a turns out to be vertex b.
The distance between vertices a and b is the diameter of the
tree.
dfs(a,
0, dista, -1);
b =
max_element(dista.begin() + 1,
dista.begin() + n + 1) - dista.begin();
Then
compute the shortest distances from vertex b and store them in the array
distb.
dfs(b,
0, distb, -1);
For
each vertex i, print the distance to the farthest vertex from it.
for (i = 1; i <= n; i++)
printf("%d ", max(dista[i], distb[i]));
printf("\n");
Python implementation
Increase the recursion stack size.
import sys
sys.setrecursionlimit(1000000)
The function dfs performs
a depth-first search starting from vertex v.
·
The parameter d represents the shortest distance from the
source to vertex v.
·
The results are stored in the array dist.
·
The parameter p indicates the parent of vertex v
during the traversal.
def dfs(v, d, dist, p =- 1):
Store
the shortest distance from the source to vertex v in dist[v].
dist[v] = d
Iterate
over all edges (v, to). For each child to
of vertex v (i.e., a vertex to that is not the parent of v),
perform a depth-first search.
for to in g[v]:
if to != p:
dfs(to, d + 1, dist, v)
The
main part of the program. Read the input data.
n = int(input())
g = [[] for _ in range(n + 1)]
dista = [0] * (n + 1)
distb = [0] * (n + 1)
Construct
an undirected tree.
for _ in range(n - 1):
u,
v = map(int, input().split())
g[u].append(v)
g[v].append(u)
Compute
the shortest distances from vertex 1. The vertex farthest from it is vertex a.
dfs(1, 0, dista)
a = dista.index(max(dista[1:]))
Next,
compute the shortest distances from vertex a and
store them in the array dista. The vertex farthest from a turns
out to be vertex b. The distance between vertices a and b
is the diameter of the tree.
dfs(a, 0, dista)
b = dista.index(max(dista[1:]))
Then
compute the shortest distances from vertex b and store them in the array
distb.
dfs(b, 0, distb)
For
each vertex i, print the distance to the farthest vertex from it.
result = [max(dista[i], distb[i]) for i in range(1, n + 1)]
print(*result)