11450. Самый
длинный маршрут полета
Ульви выиграла конкурс, и призом
является бесплатная поездка на самолете, которая может состоять из одного или
нескольких полетов через города. Конечно, Ульви хочет выбрать поездку, в
которой будет как можно больше городов.
Ульви хочет лететь из Сырьяля в
Лехмяля, чтобы посетить максимальное количество городов. Вам дан список
возможных полетов, и Вы знаете, что в сети полетов нет направленных циклов.
Вход. В первой строке находятся два
целых числа n (2 ≤ n ≤ 105) и m
(1 ≤ m ≤ 2 * 105):
количество городов и рейсов. Города пронумерованы 1, 2, …, n.
Город 1 –это Сырьяля, а город n – это Лехмяля.
Далее идут m строк с
описанием рейсов. Каждая строка содержит два целых числа a и b
(1 ≤ a, b ≤ n) – описание перелета из города a
в город b. Все рейсы совершаются только в одну сторону.
Выход. Сначала выведите максимальное
количество городов на маршруте. После этого выведите города в том порядке, в
котором они будут посещены. Вы можете вывести любое допустимое решение.
Если решений нет, выведите “IMPOSSIBLE”.
|
Пример
входа |
Пример
выхода |
|
5 5 1 2 2 5 1 3 3 4 4 5 |
4 1 3 4 5 |
РЕШЕНИЕ
графы –
топологическая сортировка
Анализ алгоритма
Поскольку ориентированный граф не содержит циклов, отсортируем его вершины
топологически.
Рассмотрим массив топологически отсортированных вершин. Будем
перебирать вершины с его конца в начало. Пусть
·
can[u] = 1, если из вершины u можно добраться
в n. Изначально
установим can[n]
= 1.
·
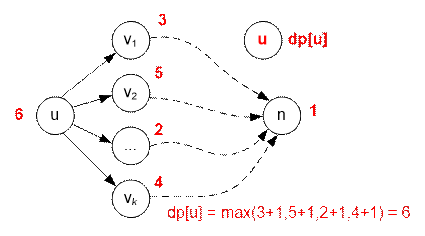
dp[u] содержит наибольшее возможное количество городов на маршруте из u в n.
Пусть u – текущая рассматриваемая вершина. Пусть v1, v2, …,
vk – вершины, в которые ведет ребро из u и из которых
достижима вершина n (для которых can[vi] = 1, 1 ≤ i ≤ k). Тогда положим
dp[u] = max(dp[vi] + 1), 1 ≤ i
≤ k
Изначально установим dp[u] = 1 (1 ≤ u
≤ n). Если из вершины u не достижима
вершина n, то так и
останется dp[u] = 1. Для
вершины n будет
установлено dp[n] = 1.
Также для каждого ребра (u, v), исходящего из u, положим can[u] = 1, если только can[v] = 1.
После обработки всех вершин dp[1] содержит наибольшее количество городов на маршруте. Выводим
сам маршрут, стартовав с v
= 1. Из текущей
вершины v двигаемся в такую вершину u, для которой существует путь в n (can[u] = 1) и для которой в n ведет самый длинный
путь (dp[v] = dp[u] + 1). Далее положим v
= u и продолжим движение пока не достигнем конечной вершины n.
Поддерживать массив can обязательно, так как иначе будет найден самый длинный
путь, который не обязательно заканчивается в вершине n. Рассмотрим, например, граф из n = 6 вершин.
Самым длинным путем будет 1 → 3 → 4 → 5, однако он не
завершается в вершине 6. Ответом на задачу будет путь 1 → 2 → 6.
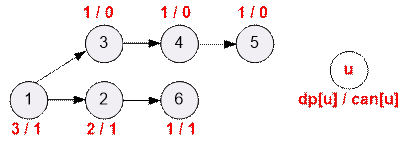
Поскольку из вершин 3, 4, 5 не достижима вершина n = 6, то для них
dp[v]
= 1, can[v] = 0.
Пример
Рассмотрим граф, приведенный в примере. Возле каждой вершины записано значение dp[v].
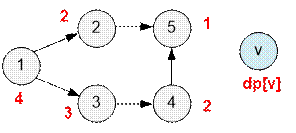
Например,
dp[4] = max(dp[2] + 1, dp[3] +
1) = max(3, 4) = 4.
Путь
1 → 3 → 4 → 5 является наибольшим.
Значение
dp[1] = 4,
следовательно максимальный путь содержит 4 вершины.
Поскольку dp[1] = 4, то из вершины 1 следует двигаться в такую соседнюю
вершину u, для которой dp[u] = 3. Такой вершиной будет u = 3.
Рассмотрим следующий тест. Возле каждой вершины запишем
значение dp[v].
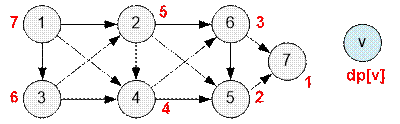
Наибольшим
путем из вершины 1 в вершину 7 будет
1
→ 3 → 2 → 4 → 6 → 5 → 7
Реализация алгоритма
Объявим рабочие массивы. Список смежности графа содержится в g.
vector<vector<int>> g;
vector<int> top, used, can, dp;
Функция dfs совершает обход в глубину из вершины v. В массиве top сохраняем топологический порядок вершин.
void dfs(int v)
{
used[v] = 1;
for (int to : g[v])
if (used[to] == 0) dfs(to);
top.push_back(v);
}
Основная часть программы. Читаем входные данные. Строим граф.
scanf("%d %d", &n, &m);
g.resize(n
+ 1);
while (m--)
{
scanf("%d %d", &a, &b);
g[a].push_back(b);
}
Запускаем поиск в глубину на ориентированном графе.
used.resize(n
+ 1);
for (i = 1; i <= n; i++)
if (used[i] == 0) dfs(i);
Обратим массив top. Теперь топологический порядок вершин начинается с
начала массива.
reverse(top.begin(),
top.end());
Инициализируем массивы.
dp.resize(n
+ 1);
can.resize(n
+ 1);
Из вершины n можно достичь вершину n.
can[n] = 1;
Перебираем вершины графа в порядке, обратном их топологической сортировки.
while (!top.empty())
{
Извлекаем и удаляем вершину из конца массива топологической сортировки.
u = top.back(); top.pop_back();
Путь из вершины u в u состоит из одной
вершины (инициализация).
dp[u] = 1;
Перебираем вершины v, смежные с u. Рассматриваем ребро (u, v).
for (int v : g[u])
Если из вершины v можно достичь вершину n при наличии ребра (u, v), то число вершин dp[u] на пути из u в n составит dp[v] + 1. Для всех таких
возможных вершин v следует найти
максимум среди dp[v]
+ 1.
Установим также can[u] = 1.
if (can[v])
{
can[u] = 1;
dp[u] = max(dp[u], dp[v] + 1);
}
}
Если из вершины 1 можно достичь вершину
n (can[1] = 1), то выводим максимальное количество городов
на маршруте и вершину 1 как стартовую на пути.
if (can[1])
printf("%d\n1 ", dp[1]);
else
{
Если вершина n не достижима, то
выводим “IMPOSSIBLE” и завершаем программу.
printf("IMPOSSIBLE\n");
return 0;
}
Выводим самый длинный путь из 1 в n. Начинаем с вершины v
= 1.
v = 1;
while (v != n)
{
Для текущей вершины v перебираем ребра (v, u).
for (int u : g[v])
{
Движение из v совершаем в такую
вершину u, для которой
существует путь в n (can[u] = 1), а также для которой в n ведет наибольший путь (dp[v] = dp[u] + 1).
if ((dp[u] + 1 ==
dp[v]) && can[u])
{
v = u;
break;
}
}
Выводим текущую вершину v.
printf("%d ", v);
}