11453. Минимальная
и максимальная
компонента связности
Задан неориентированный граф.
Найдите размер ее наименьшей и наибольшей компоненты связности.
Вход. Первая строка содержит два
натуральных числа n и m (1 ≤ n, m ≤ 10000) – количество вершин и ребер
графа. Каждая из следующих m строк содержит два целых числа ai
и bi (1 ≤ ai, bi ≤ n)
– описание неориентированного ребра.
Выход. В одной строке выведите размер
наименьшей и наибольшей компоненты связности графа.
|
Пример
входа |
Пример
выхода |
|
7 5 1 3 2 3 3 2 2 4 6 7 |
1 4 |
РЕШЕНИЕ
графы – связность
Анализ алгоритма
Запустим поиск в глубину на несвязном графе. Объявим глобальную переменную –
счетчик cnt. Внутри функции dfs при входе в вершину будем увеличивать
значение этого счетчика на 1: cnt++. Перед каждым вызовом dfs будем обнулять cnt. Таким образом при
выходе из поиска в глубину cnt будет содержать размер текущей компоненты. Перебираем все
компоненты связности и находим их размеры. Ищем наименьшее и наибольшее среди
них значения.
Пример
Рассмотрим неориентированный граф, приведенный в примере.
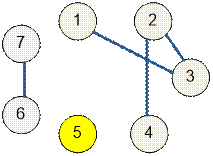
Неориентированный граф содержит три компоненты связности,
размеры которых равны 1, 2 и 4.
Реализация алгоритма
Объявим рабочие массивы. Список смежности графа содержится в g.
vector<vector<int> > g;
vector<int>
used;
Функция dfs совершает поиск в глубину из вершины v. В переменной cnt подсчитывается количество посещенных вершин в
процессе поиска.
void dfs(int v)
{
used[v] = 1;
cnt++;
for (int i = 0; i < g[v].size(); i++)
{
int to = g[v][i];
if
(!used[to])
dfs(to);
}
}
Основная часть программы. Читаем входные данные. Строим список смежности
графа.
scanf("%d %d", &n, &m);
g.resize(n
+ 1);
for (i = 1; i <= m; i++)
{
scanf("%d %d", &a, &b);
g[a].push_back(b);
g[b].push_back(a);
}
Размер наименьшей компоненты связности подсчитываем в переменной mn, размер наибольшей компоненты
связности – в переменной mx.
used.resize(n
+ 1);
mn =
1000000;
mx =
0;
Запускаем поиск в глубину на несвязном графе. Перебираем вершины от 1 до n и если вершина еще не пройдена, то запускаем из
нее поиск в глубину.
for (i = 1; i <= n; i++)
if (used[i] == 0)
{
При каждом запуске поиска в глубину следует обнулить счетчик cnt.
cnt = 0;
Если вершина i еще не просмотрена,
то запускаем из нее поиск в глубину.
dfs(i);
Пересчитываем значения mn
и mx.
if
(cnt < mn) mn = cnt;
if
(cnt > mx) mx = cnt;
}
Выводим ответ.
printf("%d %d\n", mn, mx);