11455. K special cells

You are given a matrix of size n × m with k special cells. You need to reach cell (n, m) starting from (1, 1). From any cell, you are allowed to move only to the right or down.

Each of the k special cells has a certain power. The i-th special cell has power p_i, and if you pass through this cell, you gain this power.

Your task is to find the total power that can be collected over all possible paths from (1, 1) to (n, m).

Note that:

· The power of a path is the sum of the values p_i of all special cells visited along this path.

· Regular cells that are not special have power equal to zero.

Input. The first line contains an integer t – the number of test cases.

The first line of each test case contains three integers n, m (1 ≤ n, m ≤ 10⁵) and k (1 ≤ k ≤ 10⁶), where n × m is the size of the grid, and k is the number of special cells.

Each of the next k lines contains three integers x_i, y_i (1 ≤ x_i ≤ n, 1 ≤ y_i ≤ m) and p_i (1 ≤ p_i ≤ 10⁵), where (x_i, y_i) is the position of a special cell, and p_i is its power.

Output. For each test case, print on a separate line the total power that can be collected. Since the result may be very large, output it modulo 10⁹ + 7.

Sample input

Sample output

2 2 2

1 2 4

2 1 7

SOLUTION

combinatorics

Algorithm analysis

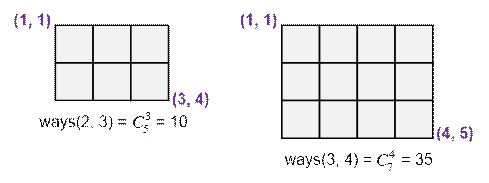
Let ways(x, y) denote the number of paths on a grid from cell (1, 1) to cell (1 + x, 1 + y). Then

ways(x, y) = =

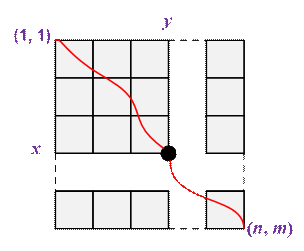
The number of paths from cell (1, 1) to cell (n, m) that pass through a special cell (x, y) is equal to ways(x – 1, y – 1) * ways(n – x, m – y). Multiplying this number by p gives the total power of all paths passing through cell (x, y).

It remains to sum the powers of all paths passing through the special cells. The answer will be equal to the sum:

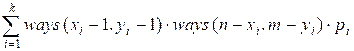
Example

In the given example, k = 2 special cells are specified.

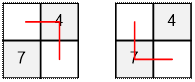
· Exactly one path passes through the cell with power 4.

· Exactly one path passes through the cell with power 7.

Thus, the total power is 4 + 7 = 11.

Algorithm implementation

Declare the arrays:

· fact contains the factorials of numbers modulo MOD,

· factinv contains the inverse values of these factorials modulo MOD:

fact[n] = n! mod 1000000007

factinv[n] = n! ^-1 mod 1000000007

#define MAX 800001

ll fact[MAX], factinv[MAX];

The pow function computes the power of a number modulo p: xⁿ mod p.

ll pow(ll x, ll n, ll p)

{

if (n == 0) return 1;

if (n % 2 == 0) return pow((x * x) % p, n / 2, p);

return (x * pow(x, n - 1, p)) % p;

}

The inverse function finds the number that is the modular inverse of x with respect to a prime modulo p. Since p is a prime number, by Fermat’s Little Theorem the following holds:

x^p^-1 mod p = 1 for any 1 ≤ x < p

This can be rewritten as (x * x^p^-2) mod p = 1, from which it follows that the modular inverse of x is x^p^-2 mod p.

ll inverse(ll x, ll p)

{

return pow(x, p - 2, p);

}

The Cnk function computes the binomial coefficient using the formula:

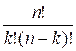
ll Cnk(int n, int k)

{

return ((fact[n] * factinv[k]) % MOD * factinv[n - k]) % MOD;

}

The ways function calculates the number of paths on an n × m grid from cell (0, 0) to cell (n, m). Since any path between these points has length n + m and contains exactly m horizontal steps, the number of paths is equal to .

ll ways(int n, int m)

{

return Cnk(n + m, m);

}

The main part of the program. Fill the arrays of factorials fact and inverse factorials factinv.

fact[0] = 1;

for (i = 1; i < MAX; i++)

fact[i] = (fact[i - 1] * i) % MOD;

factinv[0] = 1;

for (i = 1; i < MAX; i++)

factinv[i] = inverse(fact[i], MOD);

Process the tests sequentially.

scanf("%d", &tests);

while (tests--)

{

Read the data for the current test.

scanf("%d %d %d", &n, &m, &k);

Store the total obtained power in the variable res.

res = 0;

Process the k special cells.

for (i = 0; i < k; i++)

{

scanf("%d %d %d", &x, &y, &p);

res = (res + (ways(x - 1, y - 1) *

ways(n - x, m - y)) % MOD * p) % MOD;

}

Print the answer for the current test.

printf("%lld\n", res);

}