11457. Друзья Хусейна

Студент АДА Университета Хусейн Хаджиев переезжает на учебу в Сеул в университет Chung-Ang. У него там очень много друзей, все они живут на улице Heukseok-ro. Так как он будет очень часто навещать всех своих друзей, то старается найти дом поближе к ним.

Хусейн хочет минимизировать суммарное расстояние до всех своих друзей.

Вход. Первая строка содержит количество тестов.

Для каждого теста Вам задано количество друзей n (0 < n ≤ 5000) и номера домов s₁, s₂, …, s_i, …, s_n: (0 < s_i < 30000), где они живут. Обратите внимание, что по одному номеру дома могут проживать несколько друзей.

Выход. Для каждого теста выведите минимальную сумму расстояний от оптимального дома Хусейна до каждого из его друзей. Расстояние между двумя домами s_i и s_j равно d_ij = | s_i − s_j |.

Пример входа	Пример выхода
3 2 2 4 3 2 4 6 3 3 1 7	2 4 6

РЕШЕНИЕ

сортировка

Анализ алгоритма

Отсортируем номера домов n друзей. Нумерацию индексов домов будем вести с нуля: считаем, что входными номерами домов являются s₀, s₁, …, s_n-1 (s₀ ≤ s₁ ≤ … ≤ s_n-1). Если Хусейн поселится в доме x, то суммарное расстояние от него до друзей равно

f(x) = |x – s₀| + |x – s₁| + … + |x – s_n-1|

Минимум функции f(x) достигается при x = s_[n/2]. Таким образом, Хусейн должен поселиться в доме с номером s_[n/2]. Вычислим суммарное расстояние от дома s_[n/2] до домов s_i (1 £ i £ n) и выведем его.

Число x = s_[n/2] является медианой чисел s₀, s₁, …, s_n-1, то есть средним элементом при условии s₀ ≤ s₁ ≤ … ≤ s_n-1. Если n нечетное, то медиана единственная. При четном n обе медианы и все числа между ними являются оптимальными положениями для дома Хусейна.

Отметим также, что глобальный минимум функции f(x) можно найти тернарным поиском.

Пример

В первом тесте n = 2, последовательность 2, 4 имеет две медианы: 2 и 4. Дом Хусейна можно установить в позиции x, где 2 ≤ x ≤ 4. Рассмотрим функцию

f(x) = |x – 2| + |x – 4|

Вычислим некоторые значения функции:

f(0) = |0 – 2| + |0 – 4| = 2 + 4 = 6,

f(2) = |2 – 2| + |2 – 4| = 0 + 2 = 2,

f(3) = |3 – 2| + |3 – 4| = 1 + 1 = 2,

f(4) = |4 – 2| + |4 – 4| = 2 + 0 = 2,

f(6) = |6 – 2| + |6 – 4| = 4 + 2 = 6

Построим график функции:

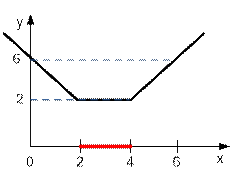
Минимум функции f(x) достигается на отрезке x ∈ [2; 4] и равен 2.

Рассмотрим третий тест. Сортируем номера домов: 1, 3, 7. Число домов n равно 3. Считаем, что s₀ = 1, s₁ = 3, s₂ = 7. Номер дома Хусейна равен s_[n/2] = s₁ = 3. Суммарное расстояние до родственников равно

f(3) = |1 – 3| + |3 – 3| + |7 – 3| = 2 + 0 + 4 = 6

График функции f(x) = |x – 1| + |x – 3| + |x – 7| имеет вид:

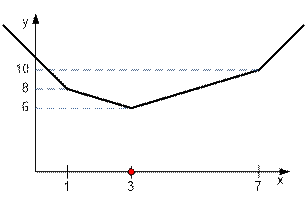
Минимум функции достигается при x = 3 и равен f(3) = 6.

Реализация алгоритма

В массиве m храним номера домов друзей s_i. При этом m[i] = s_i+1,0 £ i £ n – 1_.

int m[5001];

Для каждого теста читаем входные данные.

scanf("%d",&tests);

while(tests--)

{

scanf("%d",&n);

for(i = 0; i < n; i++)

scanf("%d",&m[i]);

Сортируем номера домов друзей.

sort(m, m + n);

Вычисляем сумму расстояний от оптимального номера дома Хусейна с номером s_[n/2] до всех остальных домов.

for(s = i = 0; i < n; i++)

s += abs(m[n/2] - m[i]);

Выводим полученную сумму.

printf("%d\n",s);

}