11461. Найдите
перестановку
Имеется последовательность A = (a1,
a2, ..., an) длины n, которая
является перестановкой 1, 2, ..., n.
Последовательность A Вам не
известна, но Вы знаете что Axi < Ayi для
m пар целых чисел (xi, yi).
Можно ли однозначно определить A?
Если можно, то найдите A.
Вход. Первая строка содержит два числа n
(2 ≤ n ≤ 2 ⋅ 105)
и m (1 ≤
m ≤ 2 ⋅ 105). Каждая из
следующих m строк содержит пару целых чисел (xi, yi),
1 ≤ xi, yi ≤ n.
Выход. Если A определяется однозначно,
то выведите Yes в первой строке. Затем во второй строке выведите a1,
a2, ..., an.
Если A не может быть определена
однозначно, то выведите No.
|
Пример
входа 1 |
Пример
выхода 1 |
|
4 4 3 1 3 4 1 4 4 2 |
Yes 2 4 1 3 |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
|
4 4 3 4 1 4 1 2 4 2 |
No |
РЕШЕНИЕ
графы – топологическая
сортировка
Анализ алгоритма
Построем граф из n вершин. Для каждого отношения Axi < Ayi построим одно ориентированное ребро xi → yi.
При помощи алгоритма Кана в массиве top найдем топологическую сортировку
графа. Если она уникальная
(на каждой итерации алгоритма очередь содержит в точности одну вершину), то последовательность A определяется
однозначно.
Неравенство Axi < Ayi означает, что элемент последовательности с индексом xi
меньше элемента последовательности с
индексом yi. Найдена топологическая сортировка на
индексах последовательности А. Теперь ее следует преобразовать в перестановку
чисел от 1 до n. Рассмотрим последовательность
неравенств:
Ax1 < Ax2 < … < Axn
Построим новый массив res, для которого res[xi] = i. Этот массив и
будет искомой перестановкой.
Пример
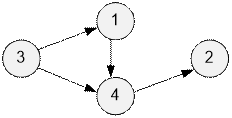
Построим граф для первого примера.
Получим единственный топологический
порядок на индексах последовательности: 3 → 1 → 4 → 2. То
есть A3 < A1
< A4 < A2. Поскольку последовательность должна содержать
перестановку чисел от 1 до n, то указанное неравенство возможно только для последовательности 1 < 2 < 3 < 4.
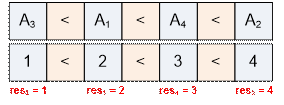
Следовательно А = res = (2, 4, 1, 3).
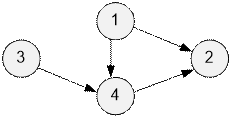
Построим граф для второго примера.
В качестве топологического
порядка можно взять последовательность 3, 1, 4, 2 или 1, 3, 4, 2. Топологическая
сортировка не является уникальной, поэтому ответ No.
Реализация алгоритма
Читаем входные данные. Строим граф. В массиве InDegree вычисляем количество ребер, входящих в каждую вершину.
scanf("%d %d", &n, &m);
g.resize(n + 1);
InDegree.resize(n +
1);
for (i = 0; i < m; i++)
{
scanf("%d %d", &a, &b);
g[a].push_back(b);
InDegree[b]++;
}
Занесем в очередь q
все вершины, в которые не ведут ребра.
for (i = 1; i < InDegree.size(); i++)
if (!InDegree[i]) q.push_back(i);
Установим flag
= 1 если топологическая сортировка уникальная, и flag =
0 в противном случае.
flag = 1;
Продолжаем работу алгоритма, пока очередь q не пуста.
while (!q.empty())
{
Если очередь q содержит более одного элемента, то топологический
порядок не уникален.
if (q.size() > 1) flag =
0;
Извлекаем вершину v из очереди и заносим ее в конец
топологического порядка top.
v = q.front(); q.pop_front();
top.push_back(v);
Удаляем из графа ребра (v, to). Для каждого такого ребра
уменьшаем входящую степень вершины to. Если степень вершины to станет
нулевой, то заносим ее в очередь, откуда она прямиком попадет в список
топологического порядка.
for (i = 0; i < g[v].size(); i++)
{
to = g[v][i];
InDegree[to]--;
if (!InDegree[to]) q.push_back(to);
}
}
В зависимости от значения flag выводим ответ.
if (flag == 1)
{
Топологический порядок уникален. Выводим сообщение Yes.
printf("Yes\n");
Преобразовываем топологический порядок индексов последовательности А в
перестановку чисел от 1 до n. Отметим, что индексация в массиве top ведется с 0.
res.resize(n + 1);
for (i = 0; i <
top.size(); i++)
res[top[i]] = i + 1;
Выводим ответ.
for (i = 1; i <
res.size(); i++)
printf("%d ", res[i]);
printf("\n");
}
else
printf("No\n");