11488. Binomial sum
Given a positive integer n. Find the
value of the next sum
Input. One positive integer n (n ≤ 30).
Output. Print the sum value.
|
Sample
input |
Sample
output |
|
3 |
20 |
SOLUTION
combinatorics
Algorithm analysis
Rewrite the sum in the form:
=
The sum in parentheses is 2n.
If in Newton’s binomial formula
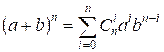
we set a = b = 1, then we get the
relation: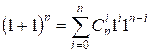 
, or
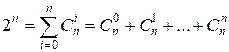
Let’s compute the
remaining sum:
=
=
=
= 
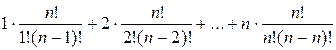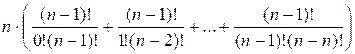So the answer is 2n + = 
.
Example
Compute the value for n = 3. For direct
calculation:
= 
= 1 + 6 + 9 + 4 = 20
When calculated
using the formula: 
= 20.
Algorithm realization
Read the input
value of n.
scanf("%lld", &n);
Compute and print the answer.
res = (1LL <<
(n - 1)) * (n + 2);
printf("%lld\n", res);
Algorithm realization – function
Declare an array to store the results: dp[n][k] =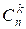 
.
int dp[31][31];
The Cnk function computes the value of the binomial
coefficient .
int Cnk(int n, int k)
{
if (n == k) return 1;
if (k == 0) return 1;
if (dp[n][k] != -1) return dp[n][k];
return dp[n][k] = (Cnk(n - 1, k - 1) + Cnk(n - 1, k)) % 9929;
}
The main part of
the program. Read the input value of n.
scanf("%d", &n);
memset(dp,
-1, sizeof(dp));
Compute the required sum.
res = 0;
for (i = 0; i <= n; i++)
res += (i + 1) * Cnk(n, i);
Print the answer.
printf("%d\n", res);
Python realization – comb
function
import math
Read the input
value of n.
n = int(input())
Compute the required
sum. To compute the binomial coefficient, we’ll use the built-in function comb.
res = 0
for i in range(n + 1):
res += (i + 1) * math.comb(n, i)
Print the answer.
print(res)
Python realization – function
The Cnk function computes the value of the binomial
coefficient .
def Cnk(n, k, dp):
if n == k: return 1
if k == 0: return
1
if dp[n][k] != -1: return
dp[n][k]
dp[n][k] = Cnk(n - 1, k - 1, dp) + Cnk(n - 1, k, dp)
return dp[n][k]
The main part of
the program. Read the input value of n.
n = int(input())
Initialize all the elements of the two-dimensional
list dp with the value -1. We shall use this list to memoize the results: dp[n][k] = .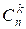
dp = [[-1 for _ in range(31)] for _ in range(31)]
Compute the required sum.
res = 0
for i in range(n + 1):
res += (i + 1) * Cnk(n, i, dp)
Print the answer.
print(res)
Python realization – formula
Read the input
value of n.
n = int(input())
Compute
the answer res using the
formula.
res = (1 <<
(n - 1)) * (n + 2)
Print the answer.
print(res)