11550. x1 + x2 + … + xk = n

 

По заданным значениям k и n найдите количество натуральных решений уравнения

x1 ​+ x2 + ...+ xk = n

 

Вход. Два натуральных числа k и n (k ≤ n ≤ 100).

 

Выход. Выведите количество натуральных решений для заданного уравнения. Известно, что ответ не превышает 1018.

 

Пример входа

Пример выхода

3 4

3

 

 

РЕШЕНИЕ

комбинаторика

 

Анализ алгоритма

Рассмотрим последовательность из n единиц: 111…11. Между любыми двумя единицами можно вставить знак ‘+’. Например 11+111+1. Такая запись будет обозначать сумму 2 + 3 + 1, где каждое слагаемое – количество единиц, стоящих рядом. Количество позиций, куда можно вставить знак ‘+’, равно n – 1. Поскольку необходимо получить сумму из k слагаемых, то следует вставить k – 1 знак ‘+’.

Нам следует вставить k – 1 плюс на n – 1 место. Это можно сделать  способами.

 

Пример

Рассмотрим уравнение x1 ​+ x2 + x3 = 4. Оно имеет 3 положительных целочисленных решения: (1, 1, 2), (1, 2, 1), (2, 1, 1).

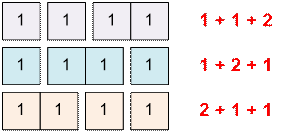
Например, n = 4 единицы на k = 3 слагаемых можно разбить  = 3 способами:

 

Реализация алгоритма

Функция Cnk вычисляет значение биномиального коэффициента .

 

long long Cnk(long long k, long long n)

{

  long long res = 1;

  if (k > n - k) k = n - k;

  for (long long i = 1; i <= k; i++)

    res = res * (n - i + 1) / i;

  return res;

}

 

Основная часть программы. Читаем входные данные.

 

scanf("%lld %lld", &k, &n);

 

Вычисляем и выводим ответ .

 

res = Cnk(k - 1, n - 1);

printf("%lld\n", res);

 

Python реализация

 

import math

 

Читаем входные данные.

 

k, n = map(int,input().split())

 

Вычисляем и выводим ответ .

 

res = math.comb(n - 1, k - 1)

print(res)