11550. x1 + x2 + … + xk = n
Given the values of k and n,
find the number of positive integral solutions for the equation
x1 + x2 + ...+ xk = n
Input. Two positive integers k and n
(k ≤ n ≤ 100).
Output. Print the number of positive integral solutions for
the given equation. It is known that the answer is no more than 1018.
|
Sample
input |
Sample
output |
|
3 4 |
3 |
SOLUTION
combinatorics
Algorithm analysis
Consider a
sequence of n ones: 111…11. You can insert a ‘+’ sign between any two ones. For example, 11+111+1. Such
notation denotes the sum 2 + 3 + 1, where each term represents the number of ones adjacent to each other.
The number of positions where a ‘+’ sign can be inserted is n – 1. Since the sum must consist of k
terms, k – 1 ‘+’ signs should be inserted.
We should insert
k – 1 pluses in n – 1 places. This can be done in 
ways.
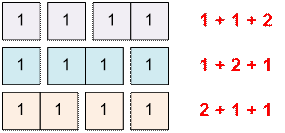
Example
Consider the equation x1
+ x2 + x3 = 4. It has 3 positive
integer solutions: (1, 1, 2), (1, 2, 1), (2, 1, 1).
For example, n = 4 ones can be divided
into k = 3 terms in 
= 3 ways:
Algorithm realization
The Cnk function computes the value of the binomial
coefficient 
.
long long Cnk(long long k, long long n)
{
long long res = 1;
if (k > n - k) k = n - k;
for (long long i = 1; i <= k; i++)
res = res * (n - i + 1) / i;
return res;
}
The main part of the program. Read the input data.
scanf("%lld %lld", &k, &n);
Compute and print the answer – the value of .
res = Cnk(k - 1, n - 1);
printf("%lld\n", res);
Python realization
import math
Read the input data.
k, n = map(int,input().split())
Compute and print the answer – the value of .
res = math.comb(n - 1, k - 1)
print(res)