11551. x₁ + x₂ + … + x_k = n (2)

По заданным значениям k и n найдите количество неотрицательных целочисленных решений уравнения

x₁ + x₂ + ...+ x_k = n

Вход. Два натуральных числа k и n (k ≤ n ≤ 100).

Выход. Выведите количество неотрицательных целочисленных решений для заданного уравнения. Известно, что ответ не превышает 10¹⁸.

Пример входа	Пример выхода
3 4	15

РЕШЕНИЕ

комбинаторика

Анализ алгоритма

Рассмотрим последовательность из n + k – 1 позиций. В n позициях следует поставить 1. В k – 1 позицию следует поставить символ ‘+’ (чтобы получить k слагаемых).

Любой расстановке единиц и знаков ‘+’ по позициям будет соответствовать некоторое решение заданного уравнения. Например, рассмотрим некоторые решения уравнения x₁ + x₂ + x₃ = 4 (4 единицы и 2 плюса):

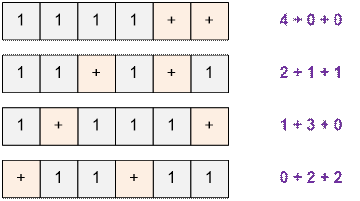
Нам следует вставить k – 1 плюс на n + k – 1 позиций. Это можно сделать способами.

Пример

Рассмотрим уравнение x₁ + x₂ + x₃ = 4. Его решениями будут:

· (4, 0, 0) и ее 3 перестановки

· (3, 1, 0) и ее 6 перестановок

· (2, 2, 0) и ее 3 перестановки

· (2, 1, 1) и ее 3 перестановки

Всего имеется 3 + 6 + 3 + 3 = 15 решений.

Реализация алгоритма

Функция Cnk вычисляет значение биномиального коэффициента .

long long Cnk(long long k, long long n)

{

long long res = 1;

if (k > n - k) k = n - k;

for (long long i = 1; i <= k; i++)

res = res * (n - i + 1) / i;

return res;

}

Основная часть программы. Читаем входные данные.

scanf("%lld %lld", &k, &n);

Вычисляем и выводим ответ .

res = Cnk(k - 1, n + k - 1);

printf("%lld\n", res);

Python реализация

import math

Читаем входные данные.

k, n = map(int,input().split())

Вычисляем и выводим ответ .

res = math.comb(n + k - 1, k - 1)

print(res)